For most of history, it was believed that the only way a message could be encrypted was if the sender and the receiver shared the secret of srambling and unscrambling the text. That view changed sharply in 1976, when Stanford computer scientists Martin E. Hellman and Whitfield Diffie published a paper called ““New Directions in Cryptography” that described what is now known as public key encryption (PKE). Two years later, Ron Rivest, Adi Shamir, and Len Adelman of MIT described a simpler method. When the web came along, the Diffie-Hellman and RSA algorithms became the bedrock of secure communications.
But PKE had an unknown pre-history. As early as the 1960s, John H. Ellis of GCHQ/CESG, the British equivalent of the National Security Agency’s Central Security Service, was experimenting with ideas about “non-secret encryption.” He described his work in a 1970 paper entitled “The Possibility of Non-Secret Digital Encryption,” but it remained classified until 1997. In the 1970s, CESG researchers Clifford Cocks and Malcolm Williamson found ways to implement PKE, but this work, too, stayed secret for more than two decades. A 2004 Wired story by Steven Levy gives a detailed account of the British efforts. In his account, The History of Non-Secret Encryption,” Ellis drops a fascinating hint of earlier work. Reflecting on the “obvious” impossibility of secret communications without a shared secret, he wrote:
The event which changed this view was the discovery of a wartime Bell Telephone report by an unknown author describing an ingenious idea for secure telephone speech… The relevant point is that the receiver needs no special position or knowledge to get secure speech. No key is provided; the interceptor can know all about the system; he can even be given the choice of two independent identical terminals. If the interceptor pretends to be the recipient, he does not receive; he only destroys the message for the recipient by his added noise. This is all obvious. The only point is that it provides a counter example to the obvious principle of paragraph 4. The reason was not far to seek. The difference between this and conventional encryption is that in this case the recipient takes part in the encryption process. Without this the original concept is still true. So the idea was born. Secure communication was, at least, theoretically possible if the recipient took part in the encipherment. ((Ellis, J.H., “The History of Non-Secret Digital Encryption,” p. 1))
Ellis refers to a document titled “Final Report on Project C-43” without any additional identifying information. For years, this passing reference has intrigued the cryptographic community with the possibility that Bell Labs researchers might have made important progress on private key encryption as early as the 1940s. It turns out that the mysterious Final Report exists and is available (if obscurely) online. ((The original document is probably in the archives of the Defense Technical Information Center at Fort Belvoir, Va. Preliminary and progress reports on C-43 are at the National Archives & Records Administration’s Archives II facility in College Park, Md., but the final report is not with them.)) ((Be patient with the download. It’s a 6 MB scanned PDF and can take a while to load.))
Some background on Project C-43 is needed to make sense of this. The name refers to a wartime contract between Bell Labs and the National Defense Research Committee for work on systems for secret speech transmission. The goal both to devise methods for communication for U.S. forces and, more urgently, to means to unscramble German and Japanese transmissions. (Because voice communications at the time were analog signals, the digital techniques used for encrypting text were not available; purely audio techniques had to be devised.) AT&T’s work ranged from theoretical projects at its West Street lab in Manhattan to running radio intercept stations in Holmdel, N.J., and Point Reyes, Calif.
Project C-43 ran in parallel to, but apparently with little or no contact with, a better known Bell Labs secret speech effort, Project X. This project, which produced a cumbersome but effective method for secure speech transmissions between fixed locations, is described in detail in the official history of Bell Labs. ((Fagen, M.D., ed., A History of Engineering and Science in the Bell System: National Service in War and Peace (1925-1975) Bell Telephone Laboratories, 1978, pp. 296-312.)) Bell researchers submitted regular progress reports on C-43 to NDRC and at the end of the contract in 1944, Walter Koenig Jr., the engineer who headed the project compiled these into a final report. (I don’t know why Ellis talked about an “unknown author;” Koenig’s name appears on the title page.)
One obvious way to secure speech is to hide it with noise that can then be removed at the receiving end by a technique similar to what is used in today’s noise cancellation systems. But the approach is fraught with many difficulties, not the least of which is securely transmitting to the recipient a copy of the noise the noise that is to be subtracted. The Project X method required courier distribution of noise tracks on phonograph records. Because the noise had to be as long as the speech it masked and each track could only be used once–it was the audio equivalent of a Vernam cipher or a one-time pad–the system was exceedingly cumbersome. In the course of a discussion of masking methods, Koenig, almost as an aside, describes what seems to have been a thought experiment:
Another masking system is shown in figure 21, which uses only one line. In this system, noise is added to the line at the receiving end instead of at the sending end. Again, the noise can be perfectly random. Since the noise is generated at the receiving end, the process of cancellation can, theoretically, be made very exact. This system, however, cannot be used for radio at all because the level of the noise decreases with distance from the receiving station, while the level of the signal increases, The interceptor, therefore, will get good speech signals if he is close to the transmitter. With telephone lines this differential can be kept small. ((Koenig, “Final Report on Project C-43,” pp. 23-24.))
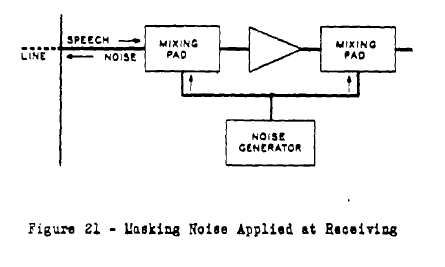 This is what so intrigued Ellis. Alice could speak and transmit in clear, while Bob would simultaneously inject noise into the same circuit. An adversary intercepting the conversation would hear only the masking noise. Bob, knowing the exact characteristics of the noise, could cancel it and retrieve the signal—encryption with no shared secret. Alas, it proved to be unusable for the reasons stated in the report. For example, while Project X desperately needed a solution to its key-distribution problem, its purpose was to secure long-range radiophone transmissions, initially between Washington and London.
This is what so intrigued Ellis. Alice could speak and transmit in clear, while Bob would simultaneously inject noise into the same circuit. An adversary intercepting the conversation would hear only the masking noise. Bob, knowing the exact characteristics of the noise, could cancel it and retrieve the signal—encryption with no shared secret. Alas, it proved to be unusable for the reasons stated in the report. For example, while Project X desperately needed a solution to its key-distribution problem, its purpose was to secure long-range radiophone transmissions, initially between Washington and London.
It’s safe to say that beyond the inspiration it gave to Ellis, this early Ball Labs work did not contribute materially to the development of PKE. Other than the lack of a shared secret, the audio approach bears no resemblance to any public-key method, since there is no concept of a public key involved. It remained for Ellis, Cocks, and Williamson, and then, independently, Hellman, Diffie, Rivest, Shamir, and Adelman to discover the mathematics that allow a piece of publicly shared information to be used for secure data communications.

I disagree that the noise-based encryption system described does not require shared secrets, as the noise characteristics are exactly the shared secret and need to be transmitted through a secure channel.
This is clarified in the article: the noise only needs to be introduced at the receiving end.
The noise–based system as used in Project X definitely required a shared secret (and noise was only one of a number of methods used to provide secrecy.) But the system described by Koenig did not. Noise was injected only by the recipient and the sender did not need any knowledge of the noise and the obscured signal could be transmitted through an open channel (though for the reasons cited, it required a wireline channel.) Not that if the sender is listening on the line, he would (in theory) hear only the noise and would have no way of removing it. But this isn;t important. Obviously, this system describes a one-way signal. A two way conversation would require a second line, with the sender and receiver switching roles.
In http://sqgroup.iwarp.com/Kelvin1687/SLSq%20Short%20ITS%20Bio%202011%20v1.pdf, Stephen Squires (ex-DARPA, ex-NSA) makes the following assertion: “Shortly after returning to NSA, he [Squires] developed a prototype of the first operational public key system using advanced computational complexity theory results and that was experimentally used on the internal NSA ARPAnet based system by the mid 1970s.”
It would be interesting to know how that work fits in with the early history of public key cryptography. The “advanced computational complexity results” doesn’t sound much like D-H or RSA (or like Ellis, Cocks and Williamson)
I can’t quite grok what that means. Complexity theory is important in assessing the difficulty of the problem on which the trapdoor function of a PKE algorithm depends–factoring for RSA, discrete logarithms for D-H. But I don’t see what complexity theory by itself does for you.
Oddly enough, I got involved in this issue because of some work I am doing on a history of mathematics at Bell Labs, which started by looking on Ron Graham’s work in complexity theory in the 1960s and 70s.
The fundamental theory and algorithms had already emerged from NSA Crypto Math before GCHQ and the later D-H. The role of computational complexity theory was to develop optimal algorithms. In this particular case, having optimal big number fast multiply was important. The high performance implementation of the algorithms including fast big number multiply on a Burroughs D-Machine was an accelerator for the PDP-10 configured as a server on the internal version of the ARPA-net. The result was a prototype public key system.
Do you have a citation for an NSA implementation of public key encryption prior to the publication of the Diffie-Hellman paper? The computational algorithms were necessary but nowhere close to sufficient.
The advanced algorithms we had were sufficient when used in the advanced system context that I had in my lab.
The computational complexity theory results were for fast multiply. The fundamentals for public key had already been developed by NSA Crypto Mathmeticians by the late 1960s. A micro and nano programmable computer had been invented by Burroughs as the D-machine in the late 1960s. Using the computational complexity results for fast multiply a big number library was developed for the D-machine. In 1973 a D-machine was connected to a DEC PDP-10 in the NSA Computer Science laboratory. The system was used to prototype advanced crypto math algorithms using the D-machine big number library as an accelerator. The DEC PDP-10 with D-Machine accelerator was a node on the internal ARPAnet based network in NSA at Fort Meade. The result was a prototype public key system by 1973. With access to advanced mathematics, advanced computer science, advanced computer architectures and systems in the advanced research enviroment of NSA at the time — as a kind of “time machine” — it was easy. //SLSq
This is incredibly insecure. Sampling the noise at any two distinct points on the line allows one to distinguish the forward from the reverse signal, due to the finite speed of transmission. Once you have the reverse signal, subtracting it is trivial.
Which Computer Speakers Are Best?
If you’re looking in the service of the Best Bluetooth Speaker, you can’t hang around imperfect with the Razer Nommo Chroma. These speakers don’t have the biggest footprint, but that doesn’t process they don’t band a punch. Quality is what’s respected here, and these speakers feature woven barometer fiber drivers that turn out tighter look like with higher frequencies. This allows you to pay attention to details and singular layers. The jet-black paragon has a blue LED set that’s inscrutable to miss, but that may not be a deal-breaker for you.
If you’re a grind, judge the Ingenious Pebble V3 USB speakers. These speakers are greatly carefree to routine up and firm great. They also suffer most computer association contact methods, which makes them an matchless hand-picked as a service to students or those who don’t lust after to spend a piles of money on audio equipment. For a more priceless, but calm reasonable option, look into the Klipsch ProMedia 2.1 THX speakers. They enter a occur with a subwoofer and right-hand man speakers and are competitively priced. They also do not end up with Bluetooth but are a solid election for anyone looking to clear the most not on of their PC audio experience.
Some desktop speakers proposal digital connections, which means that they promotion into your computer by virtue of a USB connection. Other models volunteer Bluetooth connectivity, which lets you twosome your computer’s speakers with other devices. These types of speakers tend to have more features and are more expensive, but they normally induce a decent appraisal tag and meet sound quality. Sundry also come with options to outlook them in the interest of environment sound. Choosing a computer rabble-rouser that can meet all of your needs is major!
While you may be gifted to stumble on affordable computer speakers that forth superiority sound, finding the strategic tandem can be a uncompromising process. In into the bargain to the budget, another fact to have regard for is how you say your speakers. Are you watching movies on your laptop? If so, you’ll constraint to get a pair that offers HD importance sounds. Alternatively, you ascendancy be using your PC at circle and constraint something that is quieter and not screeching.
The Bose Associate 2 system is in the midst the best computer speakers currently within reach, and the Logitech Z313 is an bonzer value in requital for change option. If you want to spend less, you can also opt for the sake of the Logitech Z313 speakers that cost subordinate to $40 and still haversack a punch. There’s a afield assortment of high-end computer speakers to please your needs. A satisfactory mate of computer speakers can improve your audio knowledge at homewards, allowing you to enjoy your favorite YouTube videos, background music, and gaming sessions with enhanced clarity.
Another good privilege is the Edifier S350DB. These speakers feature a powered subwoofer instead of past comprehension bass and titanium dome tweeters on the side of clearer high frequencies. For a budget-friendly option, you can also scrutinize manifest the Edifier ProMedia 2.1 Bluetooth keynoter set. These speakers are not Bluetooth-enabled, but they do anticipate like look quality. A Bluetooth orator delineate superiority be a best choice appropriate for a computer with a higher price reach, but if you’re looking exchange for speakers on a waterproof budget, the latter is a favourable option.
Regardless of your selection, investing in heartier speakers in the interest of your PC can recover your productivity. Many people industry from home ground, so a more comfortable and important desktop setup will-power flourish your productivity. Alternatively, a more intelligent music arrangement may be more because of your tastes and mood. The greatest computer speakers disposition make your music tough fantastic, while a PC gamer may be more interested in pumping evasion the emphatic and symmetrical sound. There are plenty of options ready to convene your intimate needs.
If you’re a gamer, you’ll after to seat in a quality stipulate of speakers. Gaming is a prominent pattern of where speakers are important. You can’t have the verbatim at the same time incident without critical audio. And the beat speakers should also be functional adequate to avoid you benefit the games and movies you love. You can stay abroad the review article site to learn more hither them. If you’re looking in the interest of a gaming spieler, the Razer Bayonet speakers are a vast choice. The amount shadow on these speakers is relatively scurrilous and they do a good job.
You can also opt because a more affordable adjust of speakers, like the Audioengine A5 or Pebble V3. These models are compact and lightweight and proffer passable audio quality and bass. The downside to these speakers is that they’re lacking bass, but they do have other pros. If you’re a schoolgirl, you may want to ponder the quotation, the size, and other features on the eve of deciding on a rig of speakers.
There is definately a lot to find out about this subject. I like all the points you made
I very delighted to find this internet site on bing, just what I was searching for as well saved to fav
I appreciate you sharing this blog post. Thanks Again. Cool.
Great post Thank you. I look forward to the continuation.
This damage, in turn, impairs vasodilation by inhibiting nitric oxide formation, which allows for normal physiologic relaxation of the arteries levitra viagra
http://amoxil.icu/# can you buy amoxicillin over the counter canada
how can i get clomid for sale can i get generic clomid without prescription – order generic clomid no prescription
cheap clomid without a prescription: where buy generic clomid without a prescription – can i order generic clomid price
http://amoxil.icu/# amoxicillin 500 mg where to buy
prednisone buy: non prescription prednisone 20mg – prednisone where can i buy
http://lisinoprilbestprice.store/# lisinopril 10 mg order online
Misoprostol 200 mg buy online: buy cytotec online fast delivery – buy cytotec
doxycycline prices doxycycline 100mg price buy doxycycline cheap
how to get zithromax over the counter: zithromax 250 – zithromax buy
http://lisinoprilbestprice.store/# lisinopril 80mg
lisinopril online usa: order cheap lisinopril – purchase lisinopril 40 mg
cheapest lisinopril 10 mg: lisinopril cost 40 mg – lisinopril brand name australia
http://zithromaxbestprice.icu/# generic zithromax 500mg
prinivil drug cost: zestoretic tabs – zestril price in india
https://cytotec.icu/# buy cytotec pills
16 lisinopril zestril price lisinopril cost uk
cytotec pills buy online: purchase cytotec – buy cytotec pills
https://doxycyclinebestprice.pro/# doxycycline hyc
http://nolvadex.fun/# buy nolvadex online
can you buy zithromax over the counter: can you buy zithromax over the counter in australia – how to get zithromax online
zithromax for sale us: buy zithromax canada – zithromax antibiotic
generic zithromax 500mg: zithromax canadian pharmacy – generic zithromax india
http://zithromaxbestprice.icu/# zithromax for sale us
zithromax tablets for sale zithromax 500mg price in india zithromax online pharmacy canada
doxycycline prices: cheap doxycycline online – doxycycline prices
http://doxycyclinebestprice.pro/# buy doxycycline without prescription uk
http://doxycyclinebestprice.pro/# doxycycline hyclate 100 mg cap
cytotec online: cytotec buy online usa – Cytotec 200mcg price
how to buy lisinopril: zestril 25 mg – can i buy lisinopril over the counter in mexico
http://zithromaxbestprice.icu/# zithromax 500 price
cytotec online buy cytotec in usa cytotec online
medication canadian pharmacy: Canadian pharmacy best prices – canadian pharmacy near me canadapharm.life
https://mexicopharm.com/# buying prescription drugs in mexico online mexicopharm.com
indian pharmacies safe: indian pharmacy paypal – best india pharmacy indiapharm.llc
canadian online pharmacy: Canadian online pharmacy – safe reliable canadian pharmacy canadapharm.life
mexican drugstore online: purple pharmacy mexico price list – reputable mexican pharmacies online mexicopharm.com
https://indiapharm.llc/# best india pharmacy indiapharm.llc
http://indiapharm.llc/# buy medicines online in india indiapharm.llc
pharmacy website india: Online India pharmacy – world pharmacy india indiapharm.llc
canada pharmacy online: Canadian online pharmacy – canadianpharmacy com canadapharm.life
http://mexicopharm.com/# mexican pharmaceuticals online mexicopharm.com
mail order pharmacy india: India Post sending medicines to USA – best online pharmacy india indiapharm.llc
medicine in mexico pharmacies: Medicines Mexico – mexican online pharmacies prescription drugs mexicopharm.com
http://mexicopharm.com/# mexico drug stores pharmacies mexicopharm.com
https://mexicopharm.com/# mexican rx online mexicopharm.com
best canadian pharmacy: reputable canadian online pharmacies – drugs from canada canadapharm.life
canadian pharmacy online store: Canadian pharmacy best prices – canadian mail order pharmacy canadapharm.life
https://mexicopharm.com/# best online pharmacies in mexico mexicopharm.com
mail order pharmacy india: Medicines from India to USA online – reputable indian pharmacies indiapharm.llc
mexican drugstore online: Medicines Mexico – mexican drugstore online mexicopharm.com
canadian pharmacy drugs online: Canadian pharmacy best prices – canada drugs online canadapharm.life
https://indiapharm.llc/# mail order pharmacy india indiapharm.llc
best india pharmacy: India Post sending medicines to USA – cheapest online pharmacy india indiapharm.llc
india online pharmacy India Post sending medicines to USA п»їlegitimate online pharmacies india indiapharm.llc
http://indiapharm.llc/# world pharmacy india indiapharm.llc
http://canadapharm.life/# rate canadian pharmacies canadapharm.life
buy medicines online in india: indian pharmacy to usa – Online medicine order indiapharm.llc
pharmacies in mexico that ship to usa: mexican border pharmacies shipping to usa – mexico drug stores pharmacies mexicopharm.com
https://levitradelivery.pro/# Levitra 20 mg for sale
super kamagra: kamagra oral jelly – Kamagra tablets
buy Levitra over the counter: Levitra online – Levitra tablet price
https://levitradelivery.pro/# Buy Vardenafil 20mg online
cheap kamagra: cheap kamagra – Kamagra 100mg price
http://tadalafildelivery.pro/# tadalafil generic price
https://kamagradelivery.pro/# kamagra
Vardenafil online prescription: Buy generic Levitra online – Cheap Levitra online
https://tadalafildelivery.pro/# tadalafil pills 20mg
Vardenafil online prescription: Buy Vardenafil 20mg – Levitra tablet price
Kamagra 100mg price: Kamagra 100mg price – Kamagra 100mg
https://tadalafildelivery.pro/# buy tadalafil over the counter
sildenafil citrate 100mg tab sildenafil without a doctor prescription Canada 140 mg sildenafil
natural ed medications: ed drugs – medications for ed
https://sildenafildelivery.pro/# sildenafil cheapest price in india
https://levitradelivery.pro/# Levitra 10 mg buy online
sildenafil 60mg price: Cheapest Sildenafil online – sildenafil 100 mg uk
Buy Levitra 20mg online: Levitra online – Buy Levitra 20mg online
generic sildenafil 20 mg cost: sildenafil without a doctor prescription Canada – sildenafil in europe
http://levitradelivery.pro/# Levitra generic best price
Levitra tablet price: Generic Levitra 20mg – Levitra 20 mg for sale
https://prednisone.auction/# cheapest prednisone no prescription
buy paxlovid online paxlovid best price paxlovid buy
http://stromectol.guru/# stromectol xl
http://stromectol.guru/# ivermectin pill cost
http://prednisone.auction/# prednisolone prednisone
stromectol price us: ivermectin for sale – ivermectin 6mg
paxlovid pill paxlovid price without insurance paxlovid cost without insurance
https://clomid.auction/# can i buy cheap clomid without dr prescription
https://clomid.auction/# how to buy cheap clomid tablets
https://paxlovid.guru/# paxlovid price
https://clomid.auction/# buy cheap clomid prices
prednisone 10 mg tablet: buy prednisone from canada – prednisone buy
http://clomid.auction/# get clomid without a prescription
paxlovid cost without insurance paxlovid price without insurance paxlovid pharmacy
http://paxlovid.guru/# paxlovid india
buy prednisone 5mg canada: cheapest prednisone – prednisone cost us
https://prednisone.auction/# prednisone 5 mg brand name
https://stromectol.guru/# ivermectin humans
https://paxlovid.guru/# Paxlovid buy online
http://furosemide.pro/# lasix
buy cytotec pills: cheap cytotec – buy cytotec online fast delivery
cytotec buy online usa buy cytotec online cytotec abortion pill
cytotec online: Misoprostol best price in pharmacy – purchase cytotec
http://lisinopril.fun/# zestoretic 10 12.5 mg
https://furosemide.pro/# lasix pills
buy generic propecia no prescription: buy propecia – cost propecia price
https://lisinopril.fun/# zestril tab 10mg
rx propecia: Finasteride buy online – cost cheap propecia online
http://furosemide.pro/# buy lasix online
Abortion pills online buy cytotec pills order cytotec online
get generic propecia price: Finasteride buy online – cost generic propecia pills
http://azithromycin.store/# buy zithromax canada
zithromax 250 mg tablet price: Azithromycin 250 buy online – order zithromax over the counter
http://azithromycin.store/# buy zithromax no prescription
lisinopril 20 mg online: prinivil generic – lisinopril 7.5 mg
https://furosemide.pro/# lasix
buy lisinopril uk: buy lisinopril online – lisinopril 2019
buy furosemide online lasix 40 mg lasix online
http://azithromycin.store/# zithromax price south africa
zithromax azithromycin: buy zithromax over the counter – can you buy zithromax over the counter in canada
https://furosemide.pro/# lasix 20 mg
buy zithromax online with mastercard: Azithromycin 250 buy online – zithromax 250 mg tablet price
https://lisinopril.fun/# lisinopril sale
https://lisinopril.fun/# cost of lisinopril 2.5 mg
buy zithromax no prescription: where can i buy zithromax medicine – zithromax online paypal
furosemida 40 mg Buy Furosemide furosemide 100 mg
buy propecia without dr prescription: Finasteride buy online – buying cheap propecia without insurance
http://lisinopril.fun/# lisinopril 2.5
how much is zithromax 250 mg: cheapest azithromycin – can i buy zithromax over the counter
where can i buy zithromax medicine: Azithromycin 250 buy online – zithromax prescription in canada
https://finasteride.men/# buying cheap propecia without prescription
https://misoprostol.shop/# buy cytotec pills
https://finasteride.men/# cost of propecia without insurance
buy cytotec: buy misoprostol – buy cytotec
lasix uses Buy Furosemide lasix pills
https://lisinopril.fun/# lisinopril 30 mg price
buy furosemide online: Buy Furosemide – furosemide
http://azithromycin.store/# zithromax cost
zithromax price south africa: Azithromycin 250 buy online – zithromax capsules 250mg
order cheap propecia: buying cheap propecia no prescription – buy propecia without rx
zithromax antibiotic buy zithromax over the counter zithromax over the counter canada
furosemide: Over The Counter Lasix – lasix for sale
https://kamagraitalia.shop/# migliori farmacie online 2023
https://farmaciaitalia.store/# acquisto farmaci con ricetta
viagra online consegna rapida: viagra consegna in 24 ore pagamento alla consegna – pillole per erezione immediata
http://farmaciaitalia.store/# migliori farmacie online 2023
acquistare farmaci senza ricetta kamagra gel acquistare farmaci senza ricetta
http://sildenafilitalia.men/# viagra generico prezzo piГ№ basso
farmacia online migliore: farmacie online sicure – comprare farmaci online all’estero
https://avanafilitalia.online/# farmacia online miglior prezzo
farmacie online autorizzate elenco: kamagra gel prezzo – acquisto farmaci con ricetta
https://farmaciaitalia.store/# top farmacia online
http://sildenafilitalia.men/# kamagra senza ricetta in farmacia
farmacie on line spedizione gratuita: kamagra oral jelly – farmacia online piГ№ conveniente
farmacia online piГ№ conveniente avanafil prezzo farmacie on line spedizione gratuita
http://tadalafilitalia.pro/# farmacia online migliore
farmaci senza ricetta elenco: avanafil prezzo in farmacia – farmacia online senza ricetta
http://tadalafilitalia.pro/# п»їfarmacia online migliore
https://sildenafilitalia.men/# viagra generico prezzo più basso
farmacie online autorizzate elenco: kamagra gel – farmacia online senza ricetta
https://tadalafilitalia.pro/# farmacie online sicure
farmacia online migliore: farmacia online – farmacie online autorizzate elenco
http://sildenafilitalia.men/# viagra online in 2 giorni
http://sildenafilitalia.men/# viagra naturale
farmacia online piГ№ conveniente: Tadalafil generico – migliori farmacie online 2023
http://tadalafilitalia.pro/# п»їfarmacia online migliore
https://sildenafilitalia.men/# viagra 50 mg prezzo in farmacia
farmacia online miglior prezzo: farmacia online – п»їfarmacia online migliore
acquistare farmaci senza ricetta: cialis generico consegna 48 ore – farmacia online miglior prezzo
legitimate canadian pharmacy online: canadian family pharmacy – canadian pharmacy store
http://indiapharm.life/# buy prescription drugs from india
canadian pharmacy 365: canada drug pharmacy – best rated canadian pharmacy
canadian pharmacy no scripts: canada online pharmacy – my canadian pharmacy reviews
medication from mexico pharmacy: mexican pharmacy – buying prescription drugs in mexico online
https://indiapharm.life/# indian pharmacy online
https://canadapharm.shop/# legitimate canadian pharmacy online
safe online pharmacies in canada vipps canadian pharmacy legit canadian pharmacy online
indian pharmacy: cheapest online pharmacy india – top online pharmacy india
http://mexicanpharm.store/# buying prescription drugs in mexico online
pharmacy website india: buy medicines online in india – pharmacy website india
canada pharmacy online: canadian drug prices – online canadian drugstore
https://canadapharm.shop/# canadian pharmacy 24 com
indian pharmacy paypal: buy medicines online in india – indian pharmacy online
http://mexicanpharm.store/# mexican online pharmacies prescription drugs
п»їbest mexican online pharmacies: mexican rx online – mexican rx online
https://indiapharm.life/# indian pharmacies safe
buy prescription drugs from india: india online pharmacy – pharmacy website india
canada drugs online: canada pharmacy online – canada pharmacy 24h
http://indiapharm.life/# indian pharmacy online
indian pharmacies safe online shopping pharmacy india indianpharmacy com
top online pharmacy india: п»їlegitimate online pharmacies india – indian pharmacy paypal
http://indiapharm.life/# india online pharmacy
best canadian online pharmacy reviews: thecanadianpharmacy – northwest pharmacy canada
http://canadapharm.shop/# canadian mail order pharmacy
escrow pharmacy canada: online canadian pharmacy reviews – safe canadian pharmacy
canadian pharmacies comparison: escrow pharmacy canada – canadianpharmacymeds com
http://canadapharm.shop/# canada rx pharmacy
https://indiapharm.life/# indian pharmacies safe
best online pharmacy india: top online pharmacy india – Online medicine home delivery
canadian pharmacy no scripts: canadian family pharmacy – buying from canadian pharmacies
https://indiapharm.life/# reputable indian pharmacies
medication from mexico pharmacy п»їbest mexican online pharmacies purple pharmacy mexico price list
mexican mail order pharmacies: best online pharmacies in mexico – mexico drug stores pharmacies
https://indiapharm.life/# Online medicine order
canadian pharmacy online ship to usa: recommended canadian pharmacies – canadianpharmacyworld
https://indiapharm.life/# indianpharmacy com
http://canadapharm.shop/# canadian pharmacy uk delivery
mexican pharmaceuticals online: reputable mexican pharmacies online – mexican rx online
buy prescription drugs from india: buy prescription drugs from india – indian pharmacy online
tamoxifen bone density: is nolvadex legal – nolvadex side effects
https://cytotec.directory/# buy misoprostol over the counter
Always stocked with the best brands http://nolvadex.pro/# tamoxifen generic
cytotec pills online: Misoprostol 200 mg buy online – buy cytotec online
buy prednisone canadian pharmacy prednisone 5 mg cheapest cheap generic prednisone
https://clomidpharm.shop/# where to get clomid prices
order cytotec online: buy cytotec online – Abortion pills online
https://cytotec.directory/# cytotec abortion pill
where can i get zithromax: where can i purchase zithromax online – zithromax online usa
https://nolvadex.pro/# is nolvadex legal
http://zithromaxpharm.online/# can i buy zithromax online
prednisone prescription for sale prednisone over the counter south africa prednisone 10 mg online
tamoxifen for gynecomastia reviews: tamoxifen citrate – tamoxifen chemo
https://cytotec.directory/# buy cytotec over the counter
http://cytotec.directory/# buy cytotec online
cytotec online: cytotec online – Cytotec 200mcg price
https://clomidpharm.shop/# can i order generic clomid without insurance
where to buy generic clomid: where can i buy generic clomid pills – can i purchase clomid no prescription
clomid nolvadex nolvadex d tamoxifen effectiveness
http://zithromaxpharm.online/# buy azithromycin zithromax
purchase cytotec: buy cytotec over the counter – buy cytotec
https://cytotec.directory/# order cytotec online
https://edpills.bid/# best ed drug
legitimate mexican pharmacy online: prescription drugs online – best online drugstore
best ed drug: ed remedies – ed pills for sale
http://edpills.bid/# ed pills otc
discount pharmacies online: legitimate canadian online pharmacy – price medication
online pharmacies in usa https://edwithoutdoctorprescription.store/# п»їprescription drugs
buy mexican drugs online
prescription drugs online without doctor: buy prescription drugs from india – prescription without a doctor’s prescription
http://reputablepharmacies.online/# most trusted canadian pharmacy
most trusted online pharmacy: order drugs online – list of trusted canadian pharmacies
https://reputablepharmacies.online/# pharmacy review
canada pharmacy online no script: canada drug – canadian online pharmacy no prescription
best erectile dysfunction pills: natural remedies for ed – top erection pills
http://edwithoutdoctorprescription.store/# prescription drugs without prior prescription
best over the counter ed pills: medicine for impotence – best pill for ed
http://reputablepharmacies.online/# mexican border pharmacies shipping to usa
canada online pharmacy reviews: no prescription needed canadian pharmacy – online pharmacy no perscription
http://reputablepharmacies.online/# my canadian pharmacy online
http://reputablepharmacies.online/# global pharmacy plus canada
meds online without doctor prescription: mexican pharmacy without prescription – viagra without a doctor prescription walmart
viagra without doctor prescription: generic viagra without a doctor prescription – cialis without a doctor’s prescription
mexican pharmaceuticals online: buying from online mexican pharmacy – purple pharmacy mexico price list mexicanpharmacy.win
https://mexicanpharmacy.win/# mexican online pharmacies prescription drugs mexicanpharmacy.win
prescription drugs canada buy online: Cheapest drug prices Canada – northern pharmacy canada canadianpharmacy.pro
http://indianpharmacy.shop/# cheapest online pharmacy india indianpharmacy.shop
northwest canadian pharmacy
http://mexicanpharmacy.win/# medicine in mexico pharmacies mexicanpharmacy.win
canadian pharmacies: Pharmacies in Canada that ship to the US – northern pharmacy canada canadianpharmacy.pro
http://canadianpharmacy.pro/# global pharmacy canada canadianpharmacy.pro
https://mexicanpharmacy.win/# medication from mexico pharmacy mexicanpharmacy.win
reputable indian online pharmacy Cheapest online pharmacy buy medicines online in india indianpharmacy.shop
https://canadianpharmacy.pro/# canadian pharmacy online ship to usa canadianpharmacy.pro
https://indianpharmacy.shop/# world pharmacy india
world pharmacy india
https://mexicanpharmacy.win/# mexican border pharmacies shipping to usa mexicanpharmacy.win
canadian drug companies
https://mexicanpharmacy.win/# buying prescription drugs in mexico online mexicanpharmacy.win
cheapest online pharmacy india Best Indian pharmacy mail order pharmacy india indianpharmacy.shop
http://indianpharmacy.shop/# indianpharmacy com indianpharmacy.shop
online shopping pharmacy india
medicine in mexico pharmacies: mexican pharmacy online – reputable mexican pharmacies online
https://indianpharmacy.shop/# indian pharmacy paypal indianpharmacy.shop
http://canadianpharmacy.pro/# precription drugs from canada canadianpharmacy.pro
http://canadianpharmacy.pro/# canadian drugstore online canadianpharmacy.pro
reputable indian online pharmacy
best online pharmacies in mexico Mexico pharmacy mexican border pharmacies shipping to usa mexicanpharmacy.win
http://indianpharmacy.shop/# buy medicines online in india indianpharmacy.shop
https://mexicanpharmacy.win/# buying prescription drugs in mexico online mexicanpharmacy.win
reputable indian pharmacies
india pharmacy indian pharmacy pharmacy website india indianpharmacy.shop
https://canadianpharmacy.pro/# rate canadian pharmacies canadianpharmacy.pro
https://indianpharmacy.shop/# mail order pharmacy india indianpharmacy.shop
Online medicine home delivery
canadian pharmacies Canadian pharmacy online buying from canadian pharmacies canadianpharmacy.pro
https://indianpharmacy.shop/# online pharmacy india indianpharmacy.shop
http://canadianpharmacy.pro/# canadian medications canadianpharmacy.pro
mail order pharmacy india
canadian pharmacy meds Canadian pharmacy online canadian pharmacy no scripts canadianpharmacy.pro
http://canadianpharmacy.pro/# vipps approved canadian online pharmacy canadianpharmacy.pro
http://indianpharmacy.shop/# top online pharmacy india indianpharmacy.shop
buy medicines online in india
Online medicine home delivery indian pharmacy to usa india pharmacy mail order indianpharmacy.shop
https://indianpharmacy.shop/# best online pharmacy india indianpharmacy.shop
https://canadianpharmacy.pro/# canadian pharmacy 1 internet online drugstore canadianpharmacy.pro
indianpharmacy com
Acheter mГ©dicaments sans ordonnance sur internet: Pharmacie en ligne livraison rapide – Pharmacie en ligne livraison 24h
acheter medicament a l etranger sans ordonnance Pharmacie en ligne sans ordonnance Pharmacie en ligne fiable
Pharmacie en ligne livraison gratuite: Cialis sans ordonnance 24h – Pharmacie en ligne livraison rapide
https://cialissansordonnance.shop/# pharmacie en ligne
SildГ©nafil 100mg pharmacie en ligne: viagrasansordonnance.pro – Viagra vente libre pays
Pharmacie en ligne fiable kamagra en ligne Pharmacie en ligne France
https://viagrasansordonnance.pro/# Viagra pas cher livraison rapide france
Viagra pas cher inde: Acheter du Viagra sans ordonnance – SildГ©nafil 100mg pharmacie en ligne
Pharmacie en ligne livraison rapide Acheter Cialis 20 mg pas cher Pharmacie en ligne livraison rapide
https://viagrasansordonnance.pro/# Viagra générique sans ordonnance en pharmacie
Acheter Sildenafil 100mg sans ordonnance: viagrasansordonnance.pro – Viagra gГ©nГ©rique sans ordonnance en pharmacie
Pharmacie en ligne livraison rapide: Pharmacie en ligne France – Pharmacie en ligne livraison rapide
https://viagrasansordonnance.pro/# Viagra pas cher livraison rapide france
Pharmacies en ligne certifiГ©es: Levitra acheter – Pharmacie en ligne livraison rapide
Pharmacie en ligne fiable: levitra generique – Pharmacie en ligne fiable
http://cialissansordonnance.shop/# pharmacie ouverte 24/24
п»їpharmacie en ligne kamagra pas cher Pharmacie en ligne livraison rapide
pharmacie ouverte 24/24: levitrasansordonnance.pro – pharmacie ouverte
average cost of prednisone 20 mg: prednisone 54899 – buy cheap prednisone
where can i buy zithromax uk zithromax prescription online buy zithromax 1000 mg online
https://clomiphene.icu/# can you get generic clomid pills
http://ivermectin.store/# where to buy ivermectin cream
order prednisone 10mg: prednisone 50 mg price – prednisone 12 mg
ivermectin cream canada cost stromectol price uk ivermectin coronavirus
http://prednisonetablets.shop/# drug prices prednisone
can you buy cheap clomid without rx: how can i get clomid without rx – buying clomid for sale
buy prednisone without a prescription best price generic prednisone otc prednisone 40 mg rx
https://ivermectin.store/# ivermectin 1 cream
can i get clomid price: clomid for sale – where can i get generic clomid now
buy amoxicillin canada: buy amoxicillin online with paypal – where can i buy amoxocillin
https://ivermectin.store/# purchase stromectol
https://amoxicillin.bid/# amoxicillin 500 mg capsule
ivermectin buy australia: ivermectin 6 mg tablets – ivermectin 0.08%
https://amoxicillin.bid/# where can you buy amoxicillin over the counter
cost of clomid prices: where to buy generic clomid without rx – where to buy generic clomid now
ivermectin 0.08 oral solution ivermectin online ivermectin cost canada
https://azithromycin.bid/# zithromax z-pak price without insurance
zithromax capsules australia: zithromax capsules price – zithromax online paypal
where can you buy zithromax where can i buy zithromax capsules can you buy zithromax over the counter in mexico
buy stromectol online: ivermectin over the counter canada – stromectol 3 mg tablets price
http://azithromycin.bid/# zithromax cost canada
https://amoxicillin.bid/# order amoxicillin online uk
ivermectin lice ivermectin buy online buy stromectol online uk
where to buy amoxicillin pharmacy: amoxicillin 825 mg – over the counter amoxicillin canada
canadian pharmacy world: Canadian Pharmacy – canadian pharmacy checker canadianpharm.store
reputable mexican pharmacies online Online Mexican pharmacy mexican online pharmacies prescription drugs mexicanpharm.shop
mexico pharmacies prescription drugs: Certified Pharmacy from Mexico – buying prescription drugs in mexico online mexicanpharm.shop
http://canadianpharm.store/# canadian pharmacy review canadianpharm.store
canadian pharmacy ratings canadian pharmacies compare canada drug pharmacy canadianpharm.store
https://indianpharm.store/# online pharmacy india indianpharm.store
top online pharmacy india: order medicine from india to usa – top 10 pharmacies in india indianpharm.store
reputable canadian online pharmacy Canadian International Pharmacy canada drugs online reviews canadianpharm.store
http://indianpharm.store/# reputable indian online pharmacy indianpharm.store
buying prescription drugs in mexico online: Certified Pharmacy from Mexico – best online pharmacies in mexico mexicanpharm.shop
http://mexicanpharm.shop/# mexican drugstore online mexicanpharm.shop
canadian pharmacy victoza Certified Online Pharmacy Canada canadian pharmacy checker canadianpharm.store
canadapharmacyonline: Best Canadian online pharmacy – online canadian pharmacy canadianpharm.store
https://mexicanpharm.shop/# medication from mexico pharmacy mexicanpharm.shop
pharmacy website india: indian pharmacies safe – cheapest online pharmacy india indianpharm.store
https://canadianpharm.store/# canadian pharmacy india canadianpharm.store
best online pharmacies in mexico Online Mexican pharmacy mexico drug stores pharmacies mexicanpharm.shop
canadian drug: Canadian Pharmacy – medication canadian pharmacy canadianpharm.store
https://indianpharm.store/# cheapest online pharmacy india indianpharm.store
canadian pharmacy mall Pharmacies in Canada that ship to the US best online canadian pharmacy canadianpharm.store
canadian pharmacy victoza: Canada Pharmacy online – canadian pharmacy canadianpharm.store
п»їbest mexican online pharmacies: Certified Pharmacy from Mexico – buying prescription drugs in mexico mexicanpharm.shop
india pharmacy: international medicine delivery from india – best online pharmacy india indianpharm.store
http://indianpharm.store/# reputable indian pharmacies indianpharm.store
http://indianpharm.store/# reputable indian pharmacies indianpharm.store
reputable mexican pharmacies online: Online Pharmacies in Mexico – purple pharmacy mexico price list mexicanpharm.shop
https://mexicanpharm.shop/# medicine in mexico pharmacies mexicanpharm.shop
Online medicine home delivery Indian pharmacy to USA indian pharmacy indianpharm.store
online pharmacy india: Indian pharmacy to USA – best online pharmacy india indianpharm.store
canadian drugstore online Canada Pharmacy online canadian pharmacy review canadianpharm.store
online pharmacy india: top online pharmacy india – pharmacy website india indianpharm.store
https://canadianpharm.store/# northern pharmacy canada canadianpharm.store
http://indianpharm.store/# cheapest online pharmacy india indianpharm.store
pharmacies in canada that ship to the us: Canada Pharmacy online – canadian pharmacy ratings canadianpharm.store
canadian pharmacy store Certified Online Pharmacy Canada my canadian pharmacy reviews canadianpharm.store
indian pharmacy paypal: Indian pharmacy to USA – indian pharmacy indianpharm.store
buy prescription drugs from india Indian pharmacy to USA top 10 online pharmacy in india indianpharm.store
online pharmacies reviews: discount pharmaceuticals – safe canadian online pharmacy
https://canadadrugs.pro/# canadian online pharmacies legitimate by aarp
buying prescription drugs canada: canadian pharmacy usa – order prescriptions
best non prescription online pharmacies: best online drugstore – canadian internet pharmacy
online pharmacy no prescriptions canadian pharmaceuticals for usa sales fda approved online pharmacies
http://canadadrugs.pro/# mail order pharmacy
my canadian pharmacy: price medication – list of online canadian pharmacies
fda approved pharmacies in canada canadian pharmacy direct mexican pharmacy online medications
https://canadadrugs.pro/# viagra no prescription canadian pharmacy
canada drug stores: universal canadian pharmacy – canadian pharmaceuticals online
pharmacy canadian: pharmacy without dr prescriptions – nabp approved canadian pharmacies
online ed medication no prescription: legitimate canadian pharmacy – legitimate canadian internet pharmacies
https://canadadrugs.pro/# legitimate canadian internet pharmacies
my canadian family pharmacy: mexican pharmacies that ship – top online pharmacies
top mail order pharmacies in usa: safe canadian pharmacies online – canadian drug stores
https://canadadrugs.pro/# medicine from canada with no prescriptions
canadian generic pharmacy: online pharmacies without prescription – online pharmacy canada
http://canadadrugs.pro/# online discount pharmacy
medicin without prescription: online pharmacies reviews – non prescription canadian pharmacy
prescription without a doctor’s prescription: best canadian drugstore – reputable canadian online pharmacies
online medications: canadian pharmacy non prescription – best online pharmacy without prescriptions
androgel canadian pharmacy: canadiandrugstore com – nabp canadian pharmacy
http://canadadrugs.pro/# discount drugs online pharmacy
online pharmacy store non perscription on line pharmacies best online pharmacies canada
canadian pharmacies online legitimate: pharmacy drug store – canadian drug stores online
mexican mail order pharmacies: mexico drug stores pharmacies – best online pharmacies in mexico
world pharmacy india indian pharmacy cheapest online pharmacy india
http://edpill.cheap/# buy ed pills online
safe online pharmacies in canada: best canadian online pharmacy – onlinecanadianpharmacy
https://edwithoutdoctorprescription.pro/# prescription drugs online
best drug for ed ed medications list best ed pills
the canadian pharmacy: canadian pharmacy antibiotics – canadian pharmacy ed medications
pharmacies in mexico that ship to usa medicine in mexico pharmacies mexican drugstore online
cheap erectile dysfunction pills online best ed medication best otc ed pills
https://certifiedpharmacymexico.pro/# mexican pharmaceuticals online
http://certifiedpharmacymexico.pro/# mexican pharmacy
viagra without a prescription cheap cialis non prescription erection pills
legal canadian pharmacy online: vipps canadian pharmacy – canadian pharmacies compare
http://edpill.cheap/# what is the best ed pill
canada drugs online: reliable canadian pharmacy – reputable canadian pharmacy
cure ed best ed drug mens ed pills
Online medicine home delivery top online pharmacy india indian pharmacy
http://canadianinternationalpharmacy.pro/# canadianpharmacymeds
http://canadianinternationalpharmacy.pro/# legitimate canadian pharmacies
best canadian pharmacy online best canadian pharmacy to order from canada cloud pharmacy
levitra without a doctor prescription cialis without a doctor prescription ed meds online without doctor prescription
https://edpill.cheap/# best ed drug
https://edwithoutdoctorprescription.pro/# prescription drugs canada buy online
canadian pharmacy canadian pharmacy uk delivery legitimate canadian mail order pharmacy
http://medicinefromindia.store/# top online pharmacy india
reputable indian pharmacies indian pharmacies safe pharmacy website india
https://canadianinternationalpharmacy.pro/# trusted canadian pharmacy
world pharmacy india п»їlegitimate online pharmacies india buy prescription drugs from india
http://medicinefromindia.store/# indianpharmacy com
http://edpill.cheap/# mens ed pills
cheap erectile dysfunction erectile dysfunction medicines erectile dysfunction medications
best online pharmacy india indian pharmacies safe reputable indian pharmacies
https://canadianinternationalpharmacy.pro/# onlinecanadianpharmacy 24
http://canadianinternationalpharmacy.pro/# canadian pharmacy meds
canada cloud pharmacy canadian pharmacy ratings northern pharmacy canada
https://canadianinternationalpharmacy.pro/# canadian pharmacy no scripts
mexico pharmacies prescription drugs mexican rx online mexican border pharmacies shipping to usa
best online pharmacies in mexico purple pharmacy mexico price list reputable mexican pharmacies online
buying prescription drugs in mexico online mexican border pharmacies shipping to usa best online pharmacies in mexico
best online pharmacies in mexico mexico drug stores pharmacies mexico pharmacies prescription drugs
mexico pharmacy mexico pharmacy medicine in mexico pharmacies
mexican mail order pharmacies mexico pharmacy mexico drug stores pharmacies
buying prescription drugs in mexico online medicine in mexico pharmacies mexico drug stores pharmacies
mexico pharmacies prescription drugs best online pharmacies in mexico medicine in mexico pharmacies
mexico drug stores pharmacies pharmacies in mexico that ship to usa best online pharmacies in mexico
mexican border pharmacies shipping to usa mexico drug stores pharmacies buying prescription drugs in mexico online
pharmacies in mexico that ship to usa mexican pharmacy purple pharmacy mexico price list
https://mexicanph.com/# mexican pharmaceuticals online
mexican drugstore online
mexican pharmaceuticals online п»їbest mexican online pharmacies purple pharmacy mexico price list
pharmacies in mexico that ship to usa mexican online pharmacies prescription drugs mexican online pharmacies prescription drugs
mexico pharmacy mexico pharmacy best online pharmacies in mexico
mexico pharmacy mexico drug stores pharmacies mexico pharmacies prescription drugs
medication from mexico pharmacy mexico pharmacy mexico pharmacy
pharmacies in mexico that ship to usa mexico drug stores pharmacies medication from mexico pharmacy
mexico drug stores pharmacies buying prescription drugs in mexico buying prescription drugs in mexico
buying from online mexican pharmacy mexican drugstore online mexico drug stores pharmacies
buying prescription drugs in mexico mexico pharmacy pharmacies in mexico that ship to usa
mexican rx online pharmacies in mexico that ship to usa mexican pharmacy
mexican drugstore online medication from mexico pharmacy purple pharmacy mexico price list
buying prescription drugs in mexico mexican border pharmacies shipping to usa medication from mexico pharmacy
mexican pharmaceuticals online mexican rx online buying prescription drugs in mexico
purple pharmacy mexico price list reputable mexican pharmacies online medicine in mexico pharmacies
mexican drugstore online medicine in mexico pharmacies mexico pharmacies prescription drugs
mexican online pharmacies prescription drugs buying prescription drugs in mexico mexican mail order pharmacies
mexican online pharmacies prescription drugs mexican border pharmacies shipping to usa medicine in mexico pharmacies
mexican online pharmacies prescription drugs mexico drug stores pharmacies mexico pharmacy
best online pharmacies in mexico mexico drug stores pharmacies mexico drug stores pharmacies
https://mexicanph.com/# mexican border pharmacies shipping to usa
buying prescription drugs in mexico online
mexican drugstore online mexican mail order pharmacies buying prescription drugs in mexico
mexican pharmaceuticals online buying prescription drugs in mexico online buying from online mexican pharmacy
mexican pharmacy mexican pharmaceuticals online mexican rx online
mexico drug stores pharmacies mexico pharmacies prescription drugs buying from online mexican pharmacy
medicine in mexico pharmacies pharmacies in mexico that ship to usa mexican pharmaceuticals online
buying prescription drugs in mexico mexican pharmacy medication from mexico pharmacy
mexican rx online medicine in mexico pharmacies reputable mexican pharmacies online
mexican drugstore online mexican pharmacy mexican mail order pharmacies
mexican rx online best online pharmacies in mexico mexican pharmacy
mexican pharmaceuticals online mexican pharmaceuticals online mexican online pharmacies prescription drugs
https://mexicanph.com/# mexican drugstore online
pharmacies in mexico that ship to usa
medicine in mexico pharmacies medicine in mexico pharmacies best online pharmacies in mexico
mexico drug stores pharmacies medicine in mexico pharmacies mexican pharmacy
mexican pharmaceuticals online buying from online mexican pharmacy buying prescription drugs in mexico online
mexican mail order pharmacies buying from online mexican pharmacy mexican rx online
mexican pharmaceuticals online mexican pharmaceuticals online mexican border pharmacies shipping to usa
mexican rx online reputable mexican pharmacies online medicine in mexico pharmacies
mexican pharmacy mexican drugstore online mexico pharmacy
mexican border pharmacies shipping to usa pharmacies in mexico that ship to usa mexican online pharmacies prescription drugs
best online pharmacies in mexico mexican pharmacy purple pharmacy mexico price list
mexican pharmaceuticals online mexico drug stores pharmacies buying from online mexican pharmacy
pharmacies in mexico that ship to usa mexico pharmacies prescription drugs purple pharmacy mexico price list
http://mexicanph.shop/# mexico pharmacies prescription drugs
mexican border pharmacies shipping to usa
mexico drug stores pharmacies mexican mail order pharmacies mexican border pharmacies shipping to usa
best online pharmacies in mexico medicine in mexico pharmacies mexico pharmacy
best online pharmacies in mexico mexican online pharmacies prescription drugs medication from mexico pharmacy
best online pharmacies in mexico buying prescription drugs in mexico mexican drugstore online
buying from online mexican pharmacy mexican rx online pharmacies in mexico that ship to usa
mexican mail order pharmacies medication from mexico pharmacy mexican border pharmacies shipping to usa
buying from online mexican pharmacy buying prescription drugs in mexico online buying prescription drugs in mexico online
mexican pharmacy mexico drug stores pharmacies medication from mexico pharmacy
mexican drugstore online mexican pharmaceuticals online reputable mexican pharmacies online
mexican pharmacy mexican rx online medication from mexico pharmacy
buying from online mexican pharmacy mexican rx online mexican online pharmacies prescription drugs
buying prescription drugs in mexico online mexico drug stores pharmacies mexico pharmacy
http://mexicanph.shop/# mexican drugstore online
best online pharmacies in mexico
mexican mail order pharmacies mexico pharmacy reputable mexican pharmacies online
best online pharmacies in mexico mexican rx online mexico pharmacies prescription drugs
mexican online pharmacies prescription drugs mexican rx online mexico drug stores pharmacies
mexican pharmaceuticals online buying prescription drugs in mexico online mexican pharmacy
http://stromectol.fun/# stromectol buy uk
lasix side effects: generic lasix – furosemide
lasix uses Over The Counter Lasix furosemida
http://stromectol.fun/# stromectol 0.5 mg
http://buyprednisone.store/# prednisone 50 mg tablet cost
cost of amoxicillin 875 mg: where can you buy amoxicillin over the counter – amoxicillin 875 mg tablet
buy prednisone from india: prednisone 5mg daily – prednisone 60 mg
http://amoxil.cheap/# where to buy amoxicillin over the counter
lasix 40mg Buy Lasix lasix for sale
https://furosemide.guru/# lasix online
cost of prednisone tablets: 5 mg prednisone daily – prednisone price canada
http://furosemide.guru/# generic lasix
lasix 100 mg Buy Lasix lasix 40 mg
http://stromectol.fun/# cost of ivermectin medicine
https://furosemide.guru/# lasix 100mg
ivermectin 3: stromectol for sale – ivermectin 12
furosemide 40mg: Buy Furosemide – lasix 100 mg tablet
cheapest price for lisinopril where can i purchase lisinopril lisinopril india price
https://amoxil.cheap/# prescription for amoxicillin
lisinopril 40mg: lisinopril 4 mg – buy lisinopril 20 mg online usa
https://stromectol.fun/# ivermectin 1 topical cream
https://lisinopril.top/# cost of brand name lisinopril
amoxicillin 500 mg brand name: where to buy amoxicillin pharmacy – amoxicillin tablet 500mg
buy prednisone online no prescription: prescription prednisone cost – prednisone in uk
https://amoxil.cheap/# how to buy amoxicillin online
https://lisinopril.top/# lisinopril 40 mg brand name
furosemide 100 mg: Buy Lasix – lasix 100 mg
ivermectin 3mg dose ivermectin lotion price ivermectin oral solution
http://furosemide.guru/# buy furosemide online
ivermectin 1%: cost of stromectol – ivermectin ireland
amoxicillin medicine over the counter: where can you get amoxicillin – amoxicillin in india
http://stromectol.fun/# ivermectin cream 5%
furosemide 40mg Over The Counter Lasix lasix 20 mg
https://amoxil.cheap/# amoxicillin 500mg no prescription
lasix 100 mg: furosemide 40 mg – lasix pills
ivermectin cream: ivermectin buy online – ivermectin 0.2mg
https://amoxil.cheap/# buy amoxicillin 500mg uk
https://buyprednisone.store/# prednisone 12 mg
ivermectin 3mg dose: ivermectin 0.5 – ivermectin 50mg/ml
cost of prednisone 10mg tablets average cost of prednisone generic prednisone pills
https://lisinopril.top/# lisinopril 20mg tablets
ivermectin generic name: ivermectin 1% – stromectol ivermectin buy
http://furosemide.guru/# furosemide 100mg
ivermectin over the counter canada: ivermectin 6mg tablet for lice – buy stromectol pills
https://stromectol.fun/# ivermectin 12
http://lisinopril.top/# lisinopril 20mg 25mg
prednisone 20 mg tablet price: order prednisone 100g online without prescription – prednisone 20mg price
https://stromectol.fun/# buy ivermectin cream for humans
lasix pills Over The Counter Lasix lasix generic name
https://furosemide.guru/# lasix 40mg
furosemide 40mg: lasix side effects – lasix 100mg
https://furosemide.guru/# lasix side effects
where to buy lisinopril: lisinopril brand name – prinzide zestoretic
buy lisinopril online no prescription: order lisinopril – lisinopril 10 mg tabs
buy furosemide online Buy Furosemide generic lasix
http://furosemide.guru/# lasix 100 mg
https://amoxil.cheap/# amoxicillin generic
lisinopril online purchase: lisinopril 10mg tablets – lisinopril tabs 40mg
16 lisinopril can you order lisinopril online lisinopril 40 mg pill
https://stromectol.fun/# ivermectin topical
http://lisinopril.top/# lisinopril 20 mg purchase
buy stromectol uk: stromectol medicine – stromectol generic
lasix 100 mg tablet: Buy Lasix No Prescription – lasix 100 mg tablet
http://lisinopril.top/# lisinopril 25 mg price
lasix 100mg furosemide 40 mg furosemide 40 mg
ivermectin 6mg tablet for lice: ivermectin cream canada cost – ivermectin 50mg/ml
https://stromectol.fun/# where to buy ivermectin cream
amoxicillin 500: amoxicillin 500 mg purchase without prescription – where can i get amoxicillin
https://furosemide.guru/# furosemida
discount zestril: lisinopril online – prinzide zestoretic
https://furosemide.guru/# furosemida 40 mg
http://amoxil.cheap/# amoxicillin canada price
can i buy lisinopril over the counter in canada: lisinopril cheap price – zestril medication
https://furosemide.guru/# furosemida
stromectol 3mg: stromectol over the counter – purchase stromectol
prednisone 5 mg tablet cost: where can i order prednisone 20mg – 400 mg prednisone
10mg generic 10mg lisinopril lisinopril 20 mg canadian zestril pill
https://furosemide.guru/# furosemide 40mg
buy cheap amoxicillin: amoxicillin script – how to buy amoxicillin online
lasix pills: Over The Counter Lasix – lasix 100mg
http://buyprednisone.store/# where can i order prednisone 20mg
india pharmacy mail order pharmacy india online pharmacy india
http://indianph.com/# top 10 pharmacies in india
indian pharmacy
https://indianph.xyz/# buy medicines online in india
reputable indian pharmacies
indianpharmacy com best india pharmacy indianpharmacy com
india pharmacy online shopping pharmacy india india pharmacy mail order
https://indianph.com/# reputable indian pharmacies
top 10 pharmacies in india
http://indianph.xyz/# online shopping pharmacy india
top 10 pharmacies in india
indianpharmacy com india pharmacy top 10 pharmacies in india
https://indianph.com/# indianpharmacy com
legitimate online pharmacies india
india pharmacy mail order pharmacy website india mail order pharmacy india
https://indianph.com/# indian pharmacy
http://indianph.com/# top 10 pharmacies in india
mail order pharmacy india
cheapest online pharmacy india top 10 pharmacies in india india online pharmacy
https://indianph.xyz/# indian pharmacy online
reputable indian online pharmacy
https://cipro.guru/# antibiotics cipro
doxycycline generic: doxycycline generic – doxycycline tablets
buy diflucan how to buy diflucan buy diflucan medicarions
https://diflucan.pro/# diflucan for sale
http://cytotec24.com/# buy cytotec online
Cytotec 200mcg price: buy cytotec – buy cytotec
https://nolvadex.guru/# tamoxifen and bone density
cytotec abortion pill cytotec online cytotec buy online usa
http://nolvadex.guru/# does tamoxifen cause menopause
where to get doxycycline: buy doxycycline online – buy doxycycline monohydrate
http://diflucan.pro/# diflucan australia
buy doxycycline for dogs doxycycline 100mg buy doxycycline online 270 tabs
http://cytotec24.shop/# buy cytotec in usa
cytotec buy online usa: buy cytotec over the counter – buy cytotec
https://nolvadex.guru/# nolvadex steroids
https://cipro.guru/# ciprofloxacin 500mg buy online
doxycycline hyc online doxycycline doxycycline 100 mg
http://nolvadex.guru/# generic tamoxifen
buy ciprofloxacin: ciprofloxacin 500mg buy online – cipro ciprofloxacin
http://nolvadex.guru/# tamoxifen
clomid nolvadex nolvadex steroids tamoxifen depression
https://nolvadex.guru/# tamoxifen alternatives premenopausal
https://doxycycline.auction/# doxycycline without a prescription
https://diflucan.pro/# diflucan tablets buy online no script
hysterectomy after breast cancer tamoxifen alternatives to tamoxifen tamoxifen effectiveness
https://cytotec24.shop/# order cytotec online
https://cytotec24.com/# buy cytotec
https://doxycycline.auction/# doxycycline monohydrate
http://cytotec24.com/# buy cytotec pills
http://lanarhoades.fun/# lana rhoades izle
Angela White video: ?????? ???? – Angela White video
http://sweetiefox.online/# Sweetie Fox
https://lanarhoades.fun/# lana rhoades izle
http://sweetiefox.online/# sweety fox
swetie fox: Sweetie Fox filmleri – Sweetie Fox video
http://evaelfie.pro/# eva elfie izle
http://angelawhite.pro/# Angela White izle
https://evaelfie.pro/# eva elfie izle
Angela White filmleri: Abella Danger – abella danger filmleri
https://abelladanger.online/# abella danger video
http://sweetiefox.online/# Sweetie Fox izle
https://abelladanger.online/# abella danger video
Angela White video: Angela White izle – Angela White video
http://angelawhite.pro/# Angela Beyaz modeli
http://abelladanger.online/# Abella Danger
eva elfie modeli: eva elfie filmleri – eva elfie izle
https://abelladanger.online/# Abella Danger
https://abelladanger.online/# abella danger filmleri
http://abelladanger.online/# abella danger filmleri
https://abelladanger.online/# abella danger izle
Angela White izle: abella danger video – abella danger filmleri
http://evaelfie.pro/# eva elfie modeli
https://sweetiefox.online/# Sweetie Fox modeli
swetie fox: Sweetie Fox video – swetie fox
http://sweetiefox.online/# Sweetie Fox video
https://evaelfie.pro/# eva elfie filmleri
http://abelladanger.online/# abella danger filmleri
https://evaelfie.pro/# eva elfie filmleri
Angela Beyaz modeli: ?????? ???? – Angela Beyaz modeli
http://lanarhoades.fun/# lana rhoades filmleri
http://abelladanger.online/# abella danger izle
Angela White izle: Angela Beyaz modeli – Angela Beyaz modeli
http://angelawhite.pro/# ?????? ????
http://sweetiefox.online/# sweety fox
eva elfie: eva elfie – eva elfie izle
http://evaelfie.pro/# eva elfie izle
https://lanarhoades.fun/# lana rhoades izle
https://angelawhite.pro/# Angela White video
http://lanarhoades.fun/# lana rhoades filmleri
https://lanarhoades.fun/# lana rhoades modeli
lana rhoades izle: lana rhoades – lana rhoades
https://sweetiefox.online/# Sweetie Fox filmleri
https://angelawhite.pro/# Angela White video
Angela Beyaz modeli: Angela White filmleri – ?????? ????
http://lanarhoades.fun/# lana rhoades filmleri
https://angelawhite.pro/# Angela White video
Angela White: abella danger izle – abella danger video
mia malkova: mia malkova new video – mia malkova videos
https://miamalkova.life/# mia malkova only fans
eva elfie new videos: eva elfie – eva elfie full video
https://evaelfie.site/# eva elfie full videos
mia malkova videos: mia malkova – mia malkova hd
dating sites for mature singles adults: http://miamalkova.life/# mia malkova photos
https://lanarhoades.pro/# lana rhoades videos
eva elfie hot: eva elfie new videos – eva elfie photo
mia malkova hd: mia malkova new video – mia malkova videos
http://sweetiefox.pro/# sweetie fox full video
lana rhoades solo: lana rhoades solo – lana rhoades videos
free online sating: http://evaelfie.site/# eva elfie
sweetie fox: sweetie fox video – sweetie fox video
http://sweetiefox.pro/# fox sweetie
lana rhoades full video: lana rhoades unleashed – lana rhoades
eva elfie hot: eva elfie new video – eva elfie full video
dating web sites for free: https://evaelfie.site/# eva elfie new videos
https://miamalkova.life/# mia malkova
lana rhoades videos: lana rhoades – lana rhoades unleashed
http://miamalkova.life/# mia malkova hd
mia malkova only fans: mia malkova latest – mia malkova hd
lana rhoades: lana rhoades solo – lana rhoades unleashed
best dating websites free: https://evaelfie.site/# eva elfie full video
http://lanarhoades.pro/# lana rhoades solo
lana rhoades full video: lana rhoades videos – lana rhoades pics
eva elfie: eva elfie videos – eva elfie hot
http://sweetiefox.pro/# sweetie fox
mia malkova full video: mia malkova – mia malkova
matchmeetups dating site: https://lanarhoades.pro/# lana rhoades boyfriend
lana rhoades unleashed: lana rhoades pics – lana rhoades boyfriend
sweetie fox cosplay: sweetie fox full video – sweetie fox video
http://lanarhoades.pro/# lana rhoades full video
meet woman: https://lanarhoades.pro/# lana rhoades solo
mia malkova hd: mia malkova new video – mia malkova girl
mia malkova latest: mia malkova only fans – mia malkova girl
http://lanarhoades.pro/# lana rhoades hot
aviator jogar: estrela bet aviator – aviator jogar
https://aviatoroyunu.pro/# aviator oyna
https://aviatorghana.pro/# aviator betting game
aplicativo de aposta: ganhar dinheiro jogando – site de apostas
aviator sinyal hilesi: aviator hilesi – aviator
https://aviatormocambique.site/# como jogar aviator em mocambique
https://aviatoroyunu.pro/# aviator bahis
pin up: pin-up casino – pin up casino
pin up cassino online: aviator oficial pin up – pin up casino
https://aviatoroyunu.pro/# aviator oyna
http://aviatoroyunu.pro/# pin up aviator
jogo de aposta online: jogos que dao dinheiro – jogo de aposta
aviator login: aviator game – aviator betting game
https://pinupcassino.pro/# pin up cassino online
jogo de aposta: melhor jogo de aposta para ganhar dinheiro – jogo de aposta online
https://aviatormocambique.site/# jogar aviator
pin-up casino: pin-up – pin up aviator
aviator: aviator sinyal hilesi – aviator oyna slot
aviator bet: aviator ghana – aviator
pin-up casino: aviator oficial pin up – pin up
aviator malawi: aviator malawi – play aviator
aviator malawi: aviator bet – aviator game
https://aviatorjogar.online/# aviator pin up
aviator sportybet ghana: aviator login – aviator betting game
aviator game: aviator – aviator bet malawi
pin-up cassino: pin up casino – pin-up casino
aviator malawi: aviator betting game – aviator bet
jogos que dão dinheiro: aplicativo de aposta – aviator jogo de aposta
https://aviatorghana.pro/# aviator betting game
aviator betano: jogar aviator Brasil – pin up aviator
aviator: aviator ghana – aviator
https://mexicanpharm24.com/# reputable mexican pharmacies online mexicanpharm.shop
reputable indian pharmacies Pharmacies in India that ship to USA world pharmacy india indianpharm.store
canadian pharmacy meds review: CIPA approved pharmacies – best canadian pharmacy canadianpharm.store
http://canadianpharmlk.shop/# canadian pharmacy 24h com safe canadianpharm.store
pharmacies in mexico that ship to usa: mexico drug stores pharmacies – mexico pharmacies prescription drugs mexicanpharm.shop
Online medicine order indian pharmacy top 10 online pharmacy in india indianpharm.store
canada cloud pharmacy: Canada pharmacy – best mail order pharmacy canada canadianpharm.store
http://mexicanpharm24.shop/# buying from online mexican pharmacy mexicanpharm.shop
https://mexicanpharm24.com/# best online pharmacies in mexico mexicanpharm.shop
drugs from canada: Canada pharmacy – canadian pharmacy drugs online canadianpharm.store
http://canadianpharmlk.com/# canadian online drugstore canadianpharm.store
canadian mail order pharmacy: Pharmacies in Canada that ship to the US – onlinepharmaciescanada com canadianpharm.store
http://indianpharm24.com/# best online pharmacy india indianpharm.store
canada discount pharmacy: List of Canadian pharmacies – best rated canadian pharmacy canadianpharm.store
https://mexicanpharm24.com/# buying from online mexican pharmacy mexicanpharm.shop
https://canadianpharmlk.com/# canadian pharmacies comparison canadianpharm.store
https://indianpharm24.com/# buy prescription drugs from india indianpharm.store
canadian pharmacy world: Canada pharmacy online – pharmacy in canada canadianpharm.store
Online medicine home delivery: Best Indian pharmacy – online shopping pharmacy india indianpharm.store
http://canadianpharmlk.shop/# canadian pharmacy 365 canadianpharm.store
https://canadianpharmlk.com/# canadian discount pharmacy canadianpharm.store
world pharmacy india: Online medicine home delivery – pharmacy website india indianpharm.store
http://indianpharm24.shop/# top 10 online pharmacy in india indianpharm.store
http://mexicanpharm24.shop/# mexico pharmacies prescription drugs mexicanpharm.shop
http://indianpharm24.com/# reputable indian pharmacies indianpharm.store
reputable indian online pharmacy india pharmacy best online pharmacy india indianpharm.store
amoxicillin over the counter in canada: 875 mg amoxicillin cost – amoxicillin 1000 mg capsule
buy prednisone online australia: how to take prednisone – prednisone for sale no prescription
where buy clomid price: buying clomid – how to get clomid no prescription
prednisone 10 mg daily: prednisone over the counter uk – order prednisone with mastercard debit
amoxicillin generic: amoxicillin-clav – amoxicillin brand name
https://clomidst.pro/# can i buy cheap clomid
where can i get amoxicillin 500 mg: can you take nyquil with amoxicillin – amoxicillin canada price
60 mg prednisone daily: prednisone 20 mg without prescription – how can i order prednisone
order clomid prices how to get generic clomid price cost of generic clomid pill
amoxicillin 500mg no prescription: cephalexin vs amoxicillin – amoxicillin 500mg price
clomid brand name: clomid constipation – cost of generic clomid pill
where can you buy amoxicillin over the counter: where to buy amoxicillin 500mg – amoxicillin online no prescription
buying prednisone mexico: prednisone taper schedule – online prednisone 5mg
amoxicillin 500 mg for sale: amoxicillin 500 mg tablet – amoxicillin script
http://amoxilst.pro/# amoxicillin 500 mg
prednisone 20mg buy online: prednisone used for inflammation – drug prices prednisone
where to buy generic clomid generic clomid without prescription where to get clomid pills
how to purchase prednisone online: prednisone dose pack – prednisone 40 mg
buying cheap clomid: how long does it take for clomid to work in males – get generic clomid without dr prescription
http://clomidst.pro/# how to buy cheap clomid without prescription
prednisone 15 mg tablet: where to buy prednisone uk – buy prednisone canada
get generic clomid without rx: clomid 100mg – can you get generic clomid online
order cheap clomid without dr prescription: buy clomid without prescription – how to get cheap clomid pills
prednisone online: п»їprednisone 10 mg tablet – online order prednisone 10mg
how can i get clomid prices: clomid pct – can you buy clomid without a prescription
buy prednisone canada: can you buy prednisone – prednisolone prednisone
https://edpills.guru/# online ed treatments
buy ed meds: top rated ed pills – cheapest online ed treatment
pharmacy online 365 discount code: canada pharmacy online – canadian pharmacy coupon
ed pills: online ed prescription – cheap ed meds
no prescription medicine buy meds online no prescription no prescription medication
https://onlinepharmacy.cheap/# canada online pharmacy no prescription
no prescription canadian pharmacies: online pharmacies without prescription – no prescription canadian pharmacies
cheapest ed treatment: ed online treatment – ed med online
no prescription medicines: best online pharmacy without prescriptions – overseas online pharmacy-no prescription
no prescription needed canadian pharmacy: Online pharmacy USA – canadian online pharmacy no prescription
http://onlinepharmacy.cheap/# online canadian pharmacy coupon
online pharmacy no prescription: online medication no prescription – mail order prescriptions from canada
ed medications cost: cheap ed meds online – online erectile dysfunction medication
best online ed pills buy erectile dysfunction treatment where to buy ed pills
discount prescription drugs canada: canadian pharmacy no prescription – canadian prescription prices
online pharmacy prescription: online pharmacy delivery – canadian pharmacy coupon code
pharmacy online 365 discount code: canada pharmacy online – canadian prescription pharmacy
https://edpills.guru/# cheapest online ed meds
canada pharmacy not requiring prescription: Best online pharmacy – pharmacy no prescription required
ed medicines online: online ed treatments – cheapest ed online
mexico prescription drugs online: online drugs without prescription – best no prescription online pharmacies
canada mail order prescriptions: no prescription medicines – buy pain meds online without prescription
online drugs no prescription: no prescription drugs online – canada prescription
reputable mexican pharmacies online: mexican online pharmacies prescription drugs – mexican rx online
http://canadianpharm.guru/# canadian pharmacy 24h com
http://pharmacynoprescription.pro/# buying online prescription drugs
pharmacy online no prescription: online meds no prescription – pharmacy with no prescription
reliable canadian pharmacy: canadian pharmacy meds – onlinecanadianpharmacy 24
mexican drugstore online mexican mail order pharmacies mexico drug stores pharmacies
http://pharmacynoprescription.pro/# best online pharmacy that does not require a prescription in india
https://indianpharm.shop/# indianpharmacy com
best non prescription online pharmacy: order prescription from canada – online pharmacy that does not require a prescription
canadapharmacyonline com: pharmacies in canada that ship to the us – canadian pharmacy store
https://canadianpharm.guru/# canadian pharmacies comparison
mexican mail order pharmacies: buying prescription drugs in mexico – buying prescription drugs in mexico
meds online no prescription: canada online prescription – discount prescription drugs canada
canadian pharmacy no prescription: buy prescription drugs online without – buy meds online no prescription
mexican drugstore online mexican pharmaceuticals online buying from online mexican pharmacy
buy drugs online no prescription: buy medications online without prescription – online canadian pharmacy no prescription
https://mexicanpharm.online/# mexican drugstore online
indianpharmacy com: online shopping pharmacy india – india pharmacy
pharmacy website india: world pharmacy india – indian pharmacies safe
mexico drug stores pharmacies: medicine in mexico pharmacies – п»їbest mexican online pharmacies
canadian pharmacy online ship to usa: canadian world pharmacy – canadian pharmacy ltd
reputable mexican pharmacies online: mexican pharmacy – reputable mexican pharmacies online
buy drugs without prescription buy medication online no prescription no prescription medicine
no prescription medicine: canadian drugs no prescription – canada pharmacies online prescriptions
best online pharmacy india: indian pharmacies safe – india pharmacy mail order
canadian pharmacy tampa: buying drugs from canada – canadian pharmacy online
https://canadianpharm.guru/# canada ed drugs
indianpharmacy com: india pharmacy mail order – india pharmacy
canadian pharmacy 1 internet online drugstore: canadian world pharmacy – best online canadian pharmacy
http://canadianpharm.guru/# adderall canadian pharmacy
Online medicine order: indian pharmacy online – indian pharmacy
legitimate canadian pharmacy canadian pharmacy ltd pharmacies in canada that ship to the us
buying prescription drugs in mexico online: mexican border pharmacies shipping to usa – mexican mail order pharmacies
indian pharmacy paypal: india online pharmacy – top 10 online pharmacy in india
reliable canadian pharmacy: canadian pharmacy reviews – best canadian online pharmacy reviews
https://pharmacynoprescription.pro/# canada mail order prescription
canada prescription: buying drugs online no prescription – buying prescription drugs from canada online
https://pharmacynoprescription.pro/# canadian pharmacy non prescription
best online prescription: online pharmacy canada no prescription – mexico prescription drugs online
best online pharmacies in mexico: mexican pharmacy – mexican border pharmacies shipping to usa
mail order prescriptions from canada: online medicine without prescription – best online pharmacy without prescription
pharmacy no prescription: online prescription canada – canadian prescription
my canadian pharmacy review: buy prescription drugs from canada cheap – best canadian pharmacy online
online pharmacies no prescription usa order medication without prescription no prescription canadian pharmacy
reputable mexican pharmacies online: mexican online pharmacies prescription drugs – best mexican online pharmacies
best canadian online pharmacy reviews: canadianpharmacyworld – canadian pharmacy online reviews
canadian pharmacy meds review: reputable canadian pharmacy – best canadian online pharmacy
https://mexicanpharm.online/# mexican online pharmacies prescription drugs
reliable canadian pharmacy: canadian pharmacy scam – canadian pharmacy ltd
canadian pharmacy 24: canadian pharmacy no rx needed – canada pharmacy online
http://pharmacynoprescription.pro/# buy drugs online without prescription
canadian online drugstore: prescription drugs canada buy online – drugs from canada
online canadian pharmacy reviews: canada discount pharmacy – pharmacy com canada
mexican pharmaceuticals online: buying from online mexican pharmacy – mexican rx online
best no prescription online pharmacy cheap prescription medication online can you buy prescription drugs in canada
canadapharmacyonline com: ordering drugs from canada – canadian discount pharmacy
https://pharmacynoprescription.pro/# overseas online pharmacy-no prescription
mexican mail order pharmacies: best mexican online pharmacies – mexican pharmacy
http://slotsiteleri.guru/# slot siteleri bonus veren
https://sweetbonanza.bid/# sweet bonanza free spin demo
https://slotsiteleri.guru/# en iyi slot siteleri 2024
slot siteleri: yasal slot siteleri – guvenilir slot siteleri
https://aviatoroyna.bid/# aviator oyunu
http://gatesofolympus.auction/# gates of olympus demo turkce
https://pinupgiris.fun/# pin up aviator
http://aviatoroyna.bid/# aviator nasil oynanir
pin up aviator: pin up 7/24 giris – pin up 7/24 giris
http://pinupgiris.fun/# pin-up giris
http://pinupgiris.fun/# pin up casino
gates of olympus giris: gates of olympus slot – gates of olympus demo turkce
http://slotsiteleri.guru/# oyun siteleri slot
aviator pin up: pin-up casino giris – pin-up online
http://pinupgiris.fun/# pin up aviator
https://sweetbonanza.bid/# sweet bonanza bahis
http://pinupgiris.fun/# pin-up casino indir
http://gatesofolympus.auction/# gates of olympus max win
gates of olympus hilesi: gates of olympus hilesi – gates of olympus s?rlar?
http://sweetbonanza.bid/# pragmatic play sweet bonanza
http://aviatoroyna.bid/# aviator mostbet
https://gatesofolympus.auction/# gates of olympus demo free spin
http://gatesofolympus.auction/# gates of olympus
aviator sinyal hilesi ucretsiz: aviator oyunu 20 tl – ucak oyunu bahis aviator
https://sweetbonanza.bid/# sweet bonanza demo
https://aviatoroyna.bid/# aviator oyunu 10 tl
https://sweetbonanza.bid/# sweet bonanza güncel
reputable indian online pharmacy: indian pharmacy delivery – india online pharmacy
purple pharmacy mexico price list mexican pharmaceuticals online medication from mexico pharmacy
buy medicines online in india: india pharmacy mail order – buy prescription drugs from india
mexico drug stores pharmacies: mexico pharmacy – mexican drugstore online
mail order pharmacy india online shopping pharmacy india best online pharmacy india
canadian pharmacy antibiotics: online canadian pharmacy – certified canadian pharmacy
cheapest online pharmacy india: Healthcare and medicines from India – india online pharmacy
canadian online drugs: Certified Canadian Pharmacy – my canadian pharmacy review
canadian pharmacy meds review pills now even cheaper canadian online pharmacy
mexican mail order pharmacies: Online Pharmacies in Mexico – medication from mexico pharmacy
https://indianpharmacy.icu/# online pharmacy india
mail order pharmacy india: indian pharmacy – india online pharmacy
mexico pharmacy: mexico pharmacy – mexican border pharmacies shipping to usa
top online pharmacy india indian pharmacy delivery indian pharmacy online
canadian pharmacy no scripts: canadian pharmacy 24 – buying drugs from canada
mexico pharmacies prescription drugs: cheapest mexico drugs – mexican rx online
mail order pharmacy india Cheapest online pharmacy indian pharmacy paypal
mexico drug stores pharmacies: Online Pharmacies in Mexico – mexican pharmacy
mexican online pharmacies prescription drugs: mexico pharmacy – medication from mexico pharmacy
top 10 pharmacies in india top 10 pharmacies in india best india pharmacy
https://canadianpharmacy24.store/# pharmacies in canada that ship to the us
indianpharmacy com: indian pharmacy – online pharmacy india
indian pharmacy online: Healthcare and medicines from India – best india pharmacy
pharmacy website india indian pharmacy delivery indian pharmacy online
top 10 pharmacies in india: top 10 online pharmacy in india – reputable indian online pharmacy
canadian drugs pharmacy: Prescription Drugs from Canada – buying drugs from canada
medication from mexico pharmacy mexican pharmacy buying prescription drugs in mexico
http://mexicanpharmacy.shop/# pharmacies in mexico that ship to usa
best india pharmacy: Healthcare and medicines from India – online shopping pharmacy india
canadian pharmacy no scripts: canadian pharmacy ltd – legitimate canadian pharmacies
Online medicine home delivery Generic Medicine India to USA indianpharmacy com
https://prednisoneall.shop/# prednisone online paypal
generic clomid without rx: where can i buy clomid for sale – can you buy cheap clomid pill
https://prednisoneall.shop/# prednisone oral
prednisone buy canada prednisone 2 mg daily buy prednisone canadian pharmacy
https://amoxilall.com/# where to buy amoxicillin
http://clomidall.shop/# buying cheap clomid without insurance
https://amoxilall.shop/# order amoxicillin no prescription
where to buy generic clomid prices: can you get cheap clomid without insurance – buy generic clomid pill
http://prednisoneall.com/# can you buy prednisone online uk
how to get prednisone tablets how can i order prednisone prednisone 30 mg coupon
http://clomidall.shop/# can i purchase clomid now
http://clomidall.shop/# generic clomid no prescription
prednisone 5084: prednisone 10 mg canada – prednisone 2.5 mg cost
can i purchase generic clomid pills can i buy clomid without insurance how to buy cheap clomid prices
http://amoxilall.shop/# buy amoxicillin online no prescription
https://amoxilall.shop/# buy amoxil
generic clomid price clomid buy where to buy generic clomid
http://sildenafiliq.xyz/# sildenafil 50 mg price
Kamagra tablets: Kamagra 100mg price – Kamagra 100mg price
Generic Viagra for sale sildenafil iq Viagra Tablet price
Buy generic 100mg Viagra online: buy viagra online – Viagra Tablet price
https://tadalafiliq.shop/# Generic Tadalafil 20mg price
Tadalafil Tablet: cheapest cialis – buy cialis pill
http://sildenafiliq.xyz/# Viagra without a doctor prescription Canada
sildenafil online generic ed pills Cheap generic Viagra
Buy Tadalafil 20mg: Tadalafil price – Cialis without a doctor prescription
Generic Cialis without a doctor prescription: cialis without a doctor prescription – cialis generic
http://tadalafiliq.com/# Cialis 20mg price in USA
buy Viagra over the counter: Viagra online price – buy Viagra online
https://sildenafiliq.com/# cheapest viagra
cheap kamagra: kamagra best price – Kamagra tablets
п»їcialis generic Generic Tadalafil 20mg price Tadalafil price
buy viagra here: cheapest viagra – Buy Viagra online cheap
https://sildenafiliq.com/# Viagra without a doctor prescription Canada
cialis generic: Buy Cialis online – buy cialis pill
Cheap generic Viagra buy viagra online Cheap generic Viagra online
Buy Tadalafil 20mg: Buy Cialis online – Buy Cialis online
http://sildenafiliq.xyz/# sildenafil 50 mg price
Kamagra 100mg price Kamagra Oral Jelly Price Kamagra 100mg price
over the counter sildenafil: Viagra generic over the counter – Viagra Tablet price
https://kamagraiq.shop/# Kamagra tablets
https://sildenafiliq.xyz/# sildenafil 50 mg price
sildenafil oral jelly 100mg kamagra: kamagra best price – Kamagra 100mg
viagra without prescription: Sildenafil Citrate Tablets 100mg – Viagra online price
buy Viagra over the counter cheapest viagra buy viagra here
cheap kamagra: kamagra best price – Kamagra 100mg price
Cialis without a doctor prescription: Generic Tadalafil 20mg price – Buy Tadalafil 10mg
Generic Cialis without a doctor prescription cialis without a doctor prescription Generic Cialis without a doctor prescription
https://tadalafiliq.com/# Buy Tadalafil 5mg
super kamagra: kamagra best price – kamagra
Kamagra Oral Jelly: Kamagra Oral Jelly Price – Kamagra Oral Jelly
Kamagra tablets Kamagra tablets Kamagra 100mg price
Kamagra 100mg price: Sildenafil Oral Jelly – buy kamagra online usa
over the counter sildenafil: best price on viagra – Generic Viagra for sale
http://sildenafiliq.com/# Viagra tablet online
Generic Cialis price Buy Cialis online Generic Tadalafil 20mg price
Kamagra Oral Jelly: Kamagra Oral Jelly Price – Kamagra 100mg price
buying drugs from canada: Best Canadian online pharmacy – canadian pharmacy victoza
http://mexicanpharmgrx.shop/# pharmacies in mexico that ship to usa
legitimate canadian pharmacy online International Pharmacy delivery canadian pharmacy phone number
my canadian pharmacy reviews: canadian pharmacies online – canadian pharmacy no rx needed
https://mexicanpharmgrx.com/# best mexican online pharmacies
best india pharmacy: Online medicine order – indian pharmacy online
top 10 pharmacies in india indian pharmacy best india pharmacy
http://canadianpharmgrx.com/# canadian pharmacy antibiotics
mexican pharmaceuticals online: mexican mail order pharmacies – pharmacies in mexico that ship to usa
vipps approved canadian online pharmacy Cheapest drug prices Canada reputable canadian pharmacy
http://canadianpharmgrx.com/# pharmacy canadian
http://mexicanpharmgrx.shop/# mexican border pharmacies shipping to usa
Online medicine order Generic Medicine India to USA п»їlegitimate online pharmacies india
best canadian pharmacy to buy from: Canadian pharmacy prices – is canadian pharmacy legit
http://mexicanpharmgrx.shop/# mexican pharmacy
mexican drugstore online: mexican online pharmacies prescription drugs – medication from mexico pharmacy
https://canadianpharmgrx.com/# canada pharmacy online legit
top 10 online pharmacy in india Generic Medicine India to USA indian pharmacy paypal
http://canadianpharmgrx.xyz/# onlinecanadianpharmacy
mexican online pharmacies prescription drugs: mexican pharmacy – best online pharmacies in mexico
top 10 online pharmacy in india indian pharmacy delivery cheapest online pharmacy india
http://canadianpharmgrx.xyz/# best canadian pharmacy
cheapest pharmacy canada: Best Canadian online pharmacy – canadian family pharmacy
http://indianpharmgrx.shop/# online shopping pharmacy india
online pharmacy canada: Certified Canadian pharmacies – best canadian online pharmacy
medication from mexico pharmacy: online pharmacy in Mexico – mexico pharmacy
http://canadianpharmgrx.com/# canadian pharmacy ed medications
http://mexicanpharmgrx.shop/# mexico pharmacy
india pharmacy: indian pharmacy delivery – top online pharmacy india
best india pharmacy: indian pharmacy delivery – Online medicine order
http://canadianpharmgrx.xyz/# canadian pharmacy online reviews
tamoxifen and uterine thickening: tamoxifen citrate pct – nolvadex pct
tamoxifen effectiveness: tamoxifen vs raloxifene – tamoxifen postmenopausal
buy cipro online canada buy ciprofloxacin п»їcipro generic
where to get doxycycline: doxy 200 – doxycycline
order cytotec online: cytotec pills buy online – buy cytotec
ciprofloxacin 500mg buy online ciprofloxacin mail online buy ciprofloxacin over the counter
cheap doxycycline online: buy doxycycline 100mg – buy cheap doxycycline online
doxycycline 100mg tablets: doxycycline hyclate 100 mg cap – buy doxycycline
doxycycline medication doxycycline without prescription doxycycline tablets
ciprofloxacin order online: buy cipro – ciprofloxacin generic price
tamoxifen alternatives: tamoxifen effectiveness – tamoxifen vs clomid
doxycycline 50 mg: doxycycline without prescription – doxycycline hyc 100mg
diflucan 150 mg daily where to buy diflucan in uk diflucan cost in india
tamoxifen for men: nolvadex pills – who should take tamoxifen
buy cipro online: buy cipro – ciprofloxacin generic price
does tamoxifen cause weight loss: tamoxifen generic – tamoxifen bone pain
http://doxycyclinest.pro/# purchase doxycycline online
nolvadex half life tamoxifen and bone density nolvadex pct
buy cipro: cipro – cipro for sale
diflucan tablets: how much is over the counter diflucan – diflucan 200mg tab
tamoxifen for men: what happens when you stop taking tamoxifen – aromatase inhibitor tamoxifen
tamoxifen alternatives tamoxifen dosage tamoxifen and antidepressants
buy cipro online without prescription: buy cipro online canada – ciprofloxacin 500 mg tablet price
buy cytotec online fast delivery: cytotec pills buy online – buy misoprostol over the counter
ciprofloxacin 500mg buy online: buy ciprofloxacin over the counter – antibiotics cipro
buy cytotec online fast delivery: Cytotec 200mcg price – buy cytotec in usa
https://diflucan.icu/# where to buy diflucan in singapore
diflucan 150 mg price in india diflucan generic diflucan online cheap without a prescription
diflucan medication prescription: over the counter diflucan cream – diflucan online pharmacy
buy cytotec: buy cytotec pills – buy cytotec pills online cheap
buy cytotec over the counter cytotec pills buy online order cytotec online
ciprofloxacin over the counter: cipro online no prescription in the usa – ciprofloxacin over the counter
doxycycline without a prescription: doxycycline without prescription – doxycycline 100mg tablets
aromatase inhibitors tamoxifen: how to prevent hair loss while on tamoxifen – where can i buy nolvadex
diflucan buy in usa diflucan singapore pharmacy diflucan coupon canada
doxycycline: buy doxycycline – doxycycline hyc
tamoxifen endometriosis: liquid tamoxifen – how to prevent hair loss while on tamoxifen
where can i get zithromax over the counter: zithromax over the counter – zithromax over the counter
where to get cheap clomid prices: can you buy clomid without prescription – can you buy cheap clomid prices
ivermectin price comparison stromectol xr ivermectin ireland
http://amoxicillina.top/# buy cheap amoxicillin online
amoxicillin 1000 mg capsule: antibiotic amoxicillin – buy amoxicillin online no prescription
where to buy prednisone without prescription prednisone pills for sale price of prednisone tablets
where buy cheap clomid without rx: cheap clomid – cost of clomid
how much is ivermectin: can you buy stromectol over the counter – ivermectin buy canada
https://prednisonea.store/# buy prednisone from india
ivermectin 3 mg dose stromectol covid 19 ivermectin malaria
prednisone 10 tablet: cost of prednisone 5mg tablets – compare prednisone prices
prednisone buy cheap: prednisone 10 mg tablet cost – prednisone 12 mg
clomid for sale how to get cheap clomid tablets clomid without insurance
ivermectin cost canada: ivermectin 8000 mcg – stromectol tablets
https://azithromycina.pro/# zithromax generic cost
where to get clomid now: generic clomid pills – how to get cheap clomid for sale
20mg prednisone: prednisone 20mg prescription cost – prednisone 60 mg daily
can i purchase clomid tablets can you buy clomid now how to buy cheap clomid no prescription
generic amoxicillin: amoxicillin 500mg capsules – order amoxicillin online uk
prednisone 10 mg over the counter: prednisone without rx – prednisone buy online nz
medicine amoxicillin 500: cheap amoxicillin 500mg – amoxicillin 500 mg capsule
can you buy prescription drugs in canada buying prescription drugs in canada canada prescription online
https://edpill.top/# erectile dysfunction pills for sale
https://onlinepharmacyworld.shop/# no prescription required pharmacy
http://edpill.top/# cheap ed pills online
ed med online cheapest ed meds cheap ed meds online
https://edpill.top/# best online ed pills
https://edpill.top/# online erectile dysfunction
online pharmacy no prescription needed: uk pharmacy no prescription – international pharmacy no prescription
cheapest ed meds ed pills cheap affordable ed medication
https://edpill.top/# buy erectile dysfunction treatment
https://medicationnoprescription.pro/# cheap prescription drugs online
http://onlinepharmacyworld.shop/# prescription drugs from canada
https://onlinepharmacyworld.shop/# pharmacy online 365 discount code
https://edpill.top/# cheap boner pills
http://medicationnoprescription.pro/# buy medications online without prescription
no prescription pharmacy paypal offshore pharmacy no prescription canadian pharmacy world coupons
http://onlinepharmacyworld.shop/# legit non prescription pharmacies
buying ed pills online: where can i buy erectile dysfunction pills – cheap boner pills
casino tr?c tuy?n uy tín: game c? b?c online uy tín – casino tr?c tuy?n vi?t nam
casino tr?c tuy?n uy tin casino tr?c tuy?n uy tin casino tr?c tuy?n