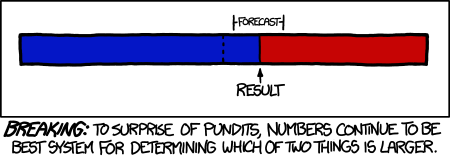
I have wanted to write about the growing importance of big data and analytics for a while, but this is a tech site and I did not want to get it embroiled in the political tempests. But now that the votes have been counted, we have a stunning demonstration of the power of data, as suggested by the XKCD cartoon above.
In the closing days of the campaign, New York Times blogger Nate Silver emerged as a lightening rod. He drew fire from both Republicans and traditional pundits of all stripes for his insistence that despite the closeness of the polls, both nationally and in key states, that President Obama was an overwhelming favorite to win re-election by a narrow margin in the popular vote and a much larger one in the electoral college. He was, of course, dead on.
People who are now hailing Silver as the greatest political pundit ever are completely missing the point, because Silver’s approach was about as far as you can get from the seat-of-the-pants, anecdotal methods of pundits. He went with the data.
Silver’s best friend was something known to mathematicians and statisticians as the law of large numbers. What this theorem, first developed in the 18th century, says is that as you take many samples some some phenomenon, say the percentage of voters supporting Obama in Ohio, the results of these tests will cluster around the true value. (The law’s cousin, the central limit theorem, allows much great specificity about the nature of that clustering, but also is subject to much more stringent restrictions.)
Pundits kept focusing on individual polls and the fact that the difference fell within the margin of error.* Silver understood that as you used more and more polls, the probable error of the aggregated result shrank. In other words (and very roughly) if 10 polls each show Candidate A with a one point lead, you can be reasonably confident that A is in the lead even though the error of each poll is plus or minus three points.
Silver also used a tool that gave him a way to quantify predictions. Now a model necessarily involves making a lot of assumptions. For example, Silver’s novel (which he has been reasonably transparent about, though he has never released its detailed specification) assigned a fairly heavy weight to key economic indicators early in the campaign, but reduced the weight as time went on based on the assumption that new data have less effect as election day nears. It also involves weighting the influence of polls based on their track record and “house effect” (a tendency to favor on party or candidate relative to other polls. He then used to model to run thousands of daily simulations of possible outcomes, a sort of Monte Carlo method. His probability of victory on any given day was simply the percentage of simulations in which a candidate emerged as the winner.
This sort of analysis has only recently become possible. First, we didn’t have the raw data. There were fewer polls, and greater lags between the collection of data and its release. Second, until the recent massive increases in cheap and available computing power, doing thousands of daily runs of a model of any complexity was impossible. A similar phenomenon lies behind the increased accuracy of weather forecasts, including the extremely accurate predictions of the course and effects of Hurricane Sandy. Weather forecasters use supercomputers for their simulations because the models are far more complex, but the techniques and the beenfits are much the same.
Too bad we don’t have more data-driven analysis in tech. Of course, there’s the big problem that a lot of the necessary data just isn’t available. Only Apple, Amazon, and Samsung know exactly how many of which products they sell, and they are not inclined to share the information. Still, there are analysts who make the most of the data. Two who come to mind are Horace Dediu of Asymco, who keeps tabs on the handset business, and Mary Meeker of Kleiner Perkins, who provides infrequent but deep data dives. We could badly use more data and less posturing.
—
*–Poll margin of error is one of the most misunderstood concepts around. First of all, the term should be abandoned. The correct concept is a confidence interval; what you are saying when you claim a margin of error is plus or minus three points is that some percentage of the time (the confidence level, typically 95% in polling) the actual result wii be within three points of the reported value. Pollster should act more like engineers and surround their point values with error bars. Second, the size of the confidence interval is purely a function of the sample size and says nothing whatever about how well a poll is executed. So a poll with poorly put questions and a badly drawn but large sample will have a tighter confidence interval than a much better done poll with a smaller sample.
Nice post. I learn something new and challenging on blogs I stumbleupon on a daily basis.
This post post made me think. I will write something about this on my blog. Have a nice day!!
This was beautiful Admin. Thank you for your reflections.
Pretty! This has been a really wonderful post. Many thanks for providing these details.
Hiya, I am really glad I have found this info. Today bloggers publish only about gossips and net and this is actually irritating. A good web site with exciting content, that is what I need. Thanks for keeping this site, I will be visiting it. Do you do newsletters? Can not find it.
Good info. Lucky me I reach on your website by accident, I bookmarked it.
Hello my friend! I wish to say that this post is amazing, nice written and include almost all important infos. I’d like to see more posts like this.
With havin so much content do you ever run into any problems of plagorism or copyright violation? My site has a lot of exclusive content I’ve either authored myself or outsourced but it looks like a lot of it is popping it up all over the web without my agreement. Do you know any methods to help protect against content from being ripped off? I’d definitely appreciate it.
With havin so much written content do you ever run into any issues of plagorism or copyright violation? My site has a lot of exclusive content I’ve either created myself or outsourced but it looks like a lot of it is popping it up all over the web without my agreement. Do you know any ways to help stop content from being stolen? I’d really appreciate it.
I appreciate, cause I found exactly what I was looking for. You’ve ended my 4 day long hunt! God Bless you man. Have a nice day. Bye
Thank you for another informative site. Where else may I am getting that type of information written in such an ideal manner? I’ve a challenge that I am simply now working on, and I have been at the glance out for such information.
Nice post. I learn something more challenging on different blogs everyday. It will always be stimulating to read content from other writers and practice a little something from their store. I’d prefer to use some with the content on my blog whether you don’t mind. Natually I’ll give you a link on your web blog. Thanks for sharing.
I do love the way you have framed this particular problem plus it does indeed offer me a lot of fodder for thought. Nevertheless, because of just what I have observed, I just wish when the reviews pile on that people remain on point and don’t get started upon a tirade involving some other news du jour. Yet, thank you for this fantastic piece and while I can not agree with this in totality, I regard your perspective.
Only a smiling visitor here to share the love (:, btw outstanding design and style.
Good – I should certainly pronounce, impressed with your site. I had no trouble navigating through all the tabs and related information ended up being truly simple to do to access. I recently found what I hoped for before you know it in the least. Quite unusual. Is likely to appreciate it for those who add forums or anything, web site theme . a tones way for your client to communicate. Excellent task.
I believe that is one of the so much significant information for me. And i’m satisfied reading your article. However wanna statement on few normal things, The web site taste is great, the articles is really great : D. Good task, cheers
I do agree with all of the ideas you have presented in your post. They’re very convincing and will definitely work. Still, the posts are too short for newbies. Could you please extend them a bit from next time? Thanks for the post.
Very nice post. I just stumbled upon your weblog and wanted to say that I’ve really enjoyed surfing around your blog posts. After all I’ll be subscribing to your rss feed and I hope you write again soon!
Perfect work you have done, this web site is really cool with excellent information.
Awsome info and right to the point. I don’t know if this is really the best place to ask but do you folks have any ideea where to hire some professional writers? Thanks in advance 🙂
As a Newbie, I am continuously browsing online for articles that can aid me. Thank you
I love your blog.. very nice colors & theme. Did you create this website yourself? Plz reply back as I’m looking to create my own blog and would like to know wheere u got this from. thanks
Nice read, I just passed this onto a colleague who was doing a little research on that. And he actually bought me lunch because I found it for him smile Thus let me rephrase that: Thanks for lunch! “A thing is not necessarily true because a man dies for it.” by Oscar Fingall O’Flahertie Wills Wilde.
You are my inhalation, I own few blogs and infrequently run out from to brand.
It’s actually a great and useful piece of information. I’m glad that you shared this useful info with us. Please keep us up to date like this. Thanks for sharing.
You could certainly see your expertise in the work you write. The world hopes for even more passionate writers like you who aren’t afraid to say how they believe. Always follow your heart.
Great wordpress blog here.. It’s hard to find quality writing like yours these days. I really appreciate people like you! take care
You have brought up a very excellent details , thankyou for the post.
I have been examinating out some of your articles and i can state clever stuff. I will make sure to bookmark your blog.
Aw, this was a very nice post. In concept I wish to put in writing like this additionally – taking time and precise effort to make an excellent article… however what can I say… I procrastinate alot and by no means appear to get one thing done.
It is really a great and useful piece of information. I am glad that you shared this helpful info with us. Please keep us informed like this. Thank you for sharing.
I really appreciate this post. I’ve been looking everywhere for this! Thank goodness I found it on Bing. You’ve made my day! Thx again!
You have brought up a very wonderful points, thankyou for the post.
Use the 1xBet promo code for registration : VIP888, and you will receive a €/$130 exclusive bonus on your first deposit. Before registering, you should familiarize yourself with the rules of the promotion.
Perfectly composed written content, thank you for selective information. “He who establishes his argument by noise and command shows that his reason is weak.” by Michel de Montaigne.
I simply had to thank you so much again. I do not know the things that I might have taken care of in the absence of those recommendations revealed by you on this situation. It previously was a troublesome problem in my view, nevertheless considering the specialised way you handled it forced me to jump for delight. Extremely thankful for this help as well as pray you know what a great job you are putting in educating some other people through the use of your webpage. I am sure you haven’t encountered any of us.
Keep up the fantastic piece of work, I read few blog posts on this site and I conceive that your web blog is real interesting and holds bands of great information.
Oh my goodness! a tremendous article dude. Thanks Nevertheless I am experiencing subject with ur rss . Don’t know why Unable to subscribe to it. Is there anyone getting similar rss downside? Anyone who is aware of kindly respond. Thnkx
You could definitely see your expertise in the work you write. The world hopes for even more passionate writers like you who are not afraid to say how they believe. Always go after your heart.
Thanx for the effort, keep up the good work Great work, I am going to start a small Blog Engine course work using your site I hope you enjoy blogging with the popular BlogEngine.net.Thethoughts you express are really awesome. Hope you will right some more posts.
Hi my loved one! I want to say that this article is amazing, great written and come with almost all vital infos. I would like to peer more posts like this.
Hi my friend! I want to say that this article is amazing, nice written and include approximately all significant infos. I would like to look extra posts like this.
Hello would you mind sharing which blog platform you’re using? I’m going to start my own blog soon but I’m having a tough time selecting between BlogEngine/Wordpress/B2evolution and Drupal. The reason I ask is because your design and style seems different then most blogs and I’m looking for something completely unique. P.S Apologies for getting off-topic but I had to ask!
Hey there, You’ve performed a great job. I will definitely digg it and individually suggest to my friends. I am sure they’ll be benefited from this website.
Howdy! Do you know if they make any plugins to help with SEO? I’m trying to get my blog to rank for some targeted keywords but I’m not seeing very good gains. If you know of any please share. Thanks!
Oh my goodness! an amazing article dude. Thanks Nonetheless I am experiencing challenge with ur rss . Don’t know why Unable to subscribe to it. Is there anybody getting similar rss problem? Anyone who is aware of kindly respond. Thnkx
I like what you guys are up too. Such smart work and reporting! Carry on the superb works guys I¦ve incorporated you guys to my blogroll. I think it’ll improve the value of my web site 🙂
Great – I should definitely pronounce, impressed with your website. I had no trouble navigating through all the tabs and related information ended up being truly easy to do to access. I recently found what I hoped for before you know it in the least. Quite unusual. Is likely to appreciate it for those who add forums or anything, web site theme . a tones way for your client to communicate. Nice task..
Very interesting information!Perfect just what I was searching for!
Greetings from California! I’m bored at work so I decided to browse your website on my iphone during lunch break. I really like the info you present here and can’t wait to take a look when I get home. I’m amazed at how fast your blog loaded on my mobile .. I’m not even using WIFI, just 3G .. Anyhow, amazing blog!
What i do not understood is actually how you’re not actually a lot more neatly-liked than you may be right now. You’re so intelligent. You know therefore considerably in terms of this topic, produced me in my opinion consider it from so many various angles. Its like women and men aren’t interested unless it is something to accomplish with Woman gaga! Your own stuffs nice. At all times take care of it up!
Hey there, You have performed a fantastic job. I’ll certainly digg it and in my opinion recommend to my friends. I am confident they’ll be benefited from this website.
I wanted to write you the tiny word so as to give thanks yet again regarding the splendid guidelines you have discussed in this case. It was quite generous of people like you to give unhampered all that many of us could possibly have made available as an electronic book to get some profit on their own, particularly given that you might well have tried it if you desired. Those ideas as well served as a great way to fully grasp some people have similar desire much like my own to see very much more with regard to this matter. I think there are lots of more pleasant periods ahead for people who take a look at your blog post.
Hi, i think that i saw you visited my weblog so i came to “return the choose”.I’m trying to to find issues to enhance my web site!I suppose its good enough to make use of a few of your concepts!!
I beloved up to you will receive performed proper here. The cartoon is attractive, your authored subject matter stylish. however, you command get got an shakiness over that you would like be handing over the following. sick undoubtedly come more earlier once more as precisely the similar nearly very incessantly inside of case you shield this hike.
I’m impressed, I need to say. Really rarely do I encounter a blog that’s each educative and entertaining, and let me let you know, you have got hit the nail on the head. Your thought is outstanding; the issue is one thing that not sufficient individuals are talking intelligently about. I’m very pleased that I stumbled throughout this in my seek for something relating to this.
It’s actually a nice and useful piece of info. I’m glad that you just shared this helpful info with us. Please stay us up to date like this. Thank you for sharing.
hi!,I like your writing so much! share we communicate more about your article on AOL? I require an expert on this area to solve my problem. May be that’s you! Looking forward to see you.
I am only writing to make you understand of the fine experience my cousin’s daughter found reading through your site. She learned too many issues, most notably how it is like to have a wonderful helping heart to have certain people just fully understand several tortuous issues. You actually exceeded visitors’ desires. I appreciate you for delivering the insightful, dependable, edifying and also unique tips about that topic to Ethel.
you have a great blog here! would you like to make some invite posts on my blog?
WONDERFUL Post.thanks for share..extra wait .. …
Wow! Thank you! I continually needed to write on my site something like that. Can I implement a fragment of your post to my blog?
I got what you intend, thanks for posting.Woh I am happy to find this website through google. “The test and use of a man’s education is that he finds pleasure in the exercise of his mind.” by Carl Barzun.
I enjoy what you guys tend to be up too. This type of clever work and reporting! Keep up the good works guys I’ve included you guys to my own blogroll.
I like what you guys are up too. Such smart work and reporting! Carry on the excellent works guys I have incorporated you guys to my blogroll. I think it will improve the value of my site 🙂
Simply wanna input on few general things, The website layout is perfect, the articles is very good : D.
great post, very informative. I’m wondering why the opposite specialists of this sector don’t notice this. You must continue your writing. I am confident, you’ve a great readers’ base already!
of course like your web site however you need to test the spelling on quite a few of your posts. Several of them are rife with spelling issues and I find it very troublesome to tell the reality nevertheless I¦ll certainly come again again.
Rattling informative and wonderful bodily structure of articles, now that’s user pleasant (:.
Some genuinely wonderful information, Gladiolus I found this.
You are a very bright individual!
Абузоустойчивый VPS
Виртуальные серверы VPS/VDS: Путь к Успешному Бизнесу
В мире современных технологий и онлайн-бизнеса важно иметь надежную инфраструктуру для развития проектов и обеспечения безопасности данных. В этой статье мы рассмотрим, почему виртуальные серверы VPS/VDS, предлагаемые по стартовой цене всего 13 рублей, являются ключом к успеху в современном бизнесе
https://withoutprescription.guru/# prescription drugs
I was wondering if you ever thought of changing the layout of your site? Its very well written; I love what youve got to say. But maybe you could a little more in the way of content so people could connect with it better. Youve got an awful lot of text for only having one or two pictures. Maybe you could space it out better?
This is the right blog for anyone who wants to find out about this topic. You realize so much its almost hard to argue with you (not that I actually would want…HaHa). You definitely put a new spin on a topic thats been written about for years. Great stuff, just great!
Thanks for some other informative web site. Where else may just I am getting that kind of information written in such a perfect approach? I’ve a project that I am simply now running on, and I’ve been on the glance out for such info.
Keep working ,splendid job!
I conceive this internet site holds very fantastic indited content material articles.
clomid for sale: where buy clomid – how can i get cheap clomid
I like what you guys are up too. Such intelligent work and reporting! Keep up the superb works guys I?¦ve incorporated you guys to my blogroll. I think it’ll improve the value of my website 🙂
п»їlegitimate online pharmacies india: indianpharmacy com – world pharmacy india
I’d should test with you here. Which isn’t one thing I usually do! I get pleasure from reading a publish that can make individuals think. Also, thanks for allowing me to remark!
https://edpills.icu/# medication for ed dysfunction
I think other web-site proprietors should take this site as an model, very clean and magnificent user genial style and design, let alone the content. You are an expert in this topic!
п»їprescription drugs: non prescription ed drugs – online prescription for ed meds
ed meds online: buy ed pills online – erection pills
buy generic clomid no prescription: buying clomid prices – cost cheap clomid without dr prescription
https://withoutprescription.guru/# ed meds online without prescription or membership
canadianpharmacyworld com: Certified and Licensed Online Pharmacy – canadian family pharmacy
I haven?¦t checked in here for a while as I thought it was getting boring, but the last several posts are good quality so I guess I?¦ll add you back to my everyday bloglist. You deserve it my friend 🙂
http://sildenafil.win/# can you purchase sildenafil over the counter
ed drugs: non prescription ed drugs – erectile dysfunction drug
best otc ed pills medicine erectile dysfunction best male enhancement pills
20 mg generic sildenafil: prices of sildenafil – sildenafil 150 mg online
Thanks for the sensible critique. Me & my neighbor were just preparing to do some research on this. We got a grab a book from our local library but I think I learned more from this post. I’m very glad to see such fantastic info being shared freely out there.
I’m now not sure the place you’re getting your information, however good topic. I must spend some time finding out more or working out more. Thanks for great information I used to be in search of this info for my mission.
https://kamagra.team/# sildenafil oral jelly 100mg kamagra
Vardenafil price Buy generic Levitra online Buy generic Levitra online
top erection pills: best ed pills online – the best ed pills
http://edpills.monster/# erectile dysfunction drug
http://levitra.icu/# Vardenafil online prescription
male erection pills ed drug prices ed drugs compared
Kamagra Oral Jelly: Kamagra tablets – sildenafil oral jelly 100mg kamagra
best ed pills online: male ed drugs – п»їerectile dysfunction medication
https://levitra.icu/# Vardenafil price
VPS SERVER
Высокоскоростной доступ в Интернет: до 1000 Мбит/с
Скорость подключения к Интернету — еще один важный фактор для успеха вашего проекта. Наши VPS/VDS-серверы, адаптированные как под Windows, так и под Linux, обеспечивают доступ в Интернет со скоростью до 1000 Мбит/с, что гарантирует быструю загрузку веб-страниц и высокую производительность онлайн-приложений на обеих операционных системах.
generic tadalafil 10mg tadalafil 10mg generic tadalafil 20 mg price canada
how much is 100mg sildenafil: 20 mg sildenafil daily – cheapest online sildenafil
https://kamagra.team/# sildenafil oral jelly 100mg kamagra
Real nice style and design and good subject material, nothing at all else we require : D.
buy Kamagra Kamagra 100mg п»їkamagra
http://tadalafil.trade/# tadalafil cheapest price
otc ed pills: new ed treatments – best ed treatment pills
sildenafil pills online: lowest prices online pharmacy sildenafil – buy sildenafil paypal
cost of generic lisinopril: Buy Lisinopril 20 mg online – prinivil tabs
http://lisinopril.auction/# zestril price uk
doxycycline 100 mg cap: Buy Doxycycline for acne – doxycycline 100mg acne
I was just seeking this info for some time. After six hours of continuous Googleing, finally I got it in your site. I wonder what’s the lack of Google strategy that do not rank this kind of informative websites in top of the list. Usually the top sites are full of garbage.
doxycycline south africa buy doxycycline online no prescription buy doxycycline pills online
п»їcipro generic: Buy ciprofloxacin 500 mg online – ciprofloxacin generic
https://amoxicillin.best/# where can i buy amoxicillin over the counter
medicine amoxicillin 500: purchase amoxicillin online – amoxicillin 250 mg price in india
zithromax for sale cheap zithromax 500 mg lowest price pharmacy online zithromax generic price
amoxicillin no prescription: buy amoxil – buy amoxicillin 500mg uk
I simply could not go away your site before suggesting that I really loved the usual info an individual supply on your visitors? Is gonna be back regularly to check up on new posts.
Wow! Thank you! I permanently wanted to write on my website something like that. Can I implement a fragment of your post to my blog?
where to buy amoxicillin amoxil for sale amoxicillin 30 capsules price
I do enjoy the way you have framed this specific problem and it does provide us some fodder for thought. Nonetheless, from what precisely I have seen, I just simply trust as the actual reviews pack on that folks continue to be on point and don’t embark upon a soap box associated with some other news du jour. Anyway, thank you for this superb piece and though I do not concur with it in totality, I respect the standpoint.
SightCare is a powerful formula that supports healthy eyes the natural way. It is specifically designed for both men and women who are suffering from poor eyesight.
buy doxycycline in india: Buy doxycycline for chlamydia – discount doxycycline
http://ciprofloxacin.men/# cipro online no prescription in the usa
ciprofloxacin generic price: Get cheapest Ciprofloxacin online – purchase cipro
doxycycline 400 mg price doxycycline buy online doxycycline iv
http://doxycycline.forum/# doxycycline brand name canada
amoxicillin 875 mg tablet purchase amoxicillin online amoxacillian without a percription
how to buy zithromax online: zithromax z-pak – can i buy zithromax over the counter in canada
https://ciprofloxacin.men/# buy cipro without rx
buy cipro online without prescription: Ciprofloxacin online prescription – cipro pharmacy
I am now not sure where you are getting your information, however great topic. I needs to spend some time learning much more or working out more. Thank you for fantastic information I was in search of this info for my mission.
Just want to say your article is as amazing. The clearness in your post is just excellent and i could assume you are an expert on this subject. Fine with your permission let me to grab your feed to keep updated with forthcoming post. Thanks a million and please keep up the gratifying work.
I am so happy to read this. This is the type of manual that needs to be given and not the accidental misinformation that’s at the other blogs. Appreciate your sharing this greatest doc.
canadian pharmacy selling viagra cheap drugs online canadian meds without a script
There may be noticeably a bundle to learn about this. I assume you made certain nice points in features also.
http://ordermedicationonline.pro/# compare medication prices
canadian pharmacy prices: certified canadian pharmacy – canada drug pharmacy
This is a topic close to my heart cheers, where are your contact details though?
canadian pharmacy online ship to usa: international online pharmacy – canada rx pharmacy
I got what you intend, thankyou for posting.Woh I am thankful to find this website through google. “I would rather be a coward than brave because people hurt you when you are brave.” by E. M. Forster.
buy medicines online in india: indian pharmacy paypal – india pharmacy mail order
https://mexicopharmacy.store/# buying prescription drugs in mexico
reliable canadian online pharmacy: accredited canadian pharmacy – www canadianonlinepharmacy
buy drugs canada buy drugs online safely canadian pharmacy online canada
As I web-site possessor I believe the content material here is rattling wonderful , appreciate it for your hard work. You should keep it up forever! Good Luck.
pharmacy website india: world pharmacy india – canadian pharmacy india
https://ordermedicationonline.pro/# canadian pharmacy
Its such as you learn my mind! You appear to understand a lot about this, such as you wrote the guide in it or something. I think that you can do with some p.c. to drive the message house a bit, however instead of that, that is fantastic blog. A fantastic read. I will definitely be back.
http://gabapentin.life/# neurontin
Boostaro is a natural health formula for men that aims to improve health.
Aizen Power is a cutting-edge male enhancement formula that improves erections and performance.
paxlovid cost without insurance: Paxlovid buy online – buy paxlovid online
Amiclear is a blood sugar support formula that’s perfect for men and women in their 30s, 40s, 50s, and even 70s.
ErecPrime is a natural male dietary supsplement designed to enhance performance and overall vitality.
Cortexi is a natural hearing support aid that has been used by thousands of people around the globe.
obviously like your web site but you have to check the spelling on several of your posts. A number of them are rife with spelling issues and I to find it very bothersome to tell the reality however I’ll definitely come back again.
Dentitox Pro is an All-Natural Liquid Oral Hygiene Supplement Consists Unique Combination Of Vitamins And Plant Extracts To Support The Health Of Gums
I like this weblog so much, saved to my bookmarks.
GlucoTrust 75% off for sale. GlucoTrust is a dietary supplement that has been designed to support healthy blood sugar levels and promote weight loss in a natural way.
https://gabapentin.life/# neurontin buy online
can you buy generic clomid online: Clomiphene Citrate 50 Mg – can you buy generic clomid for sale
Quietum Plus is a 100% natural supplement designed to address ear ringing and other hearing issues. This formula uses only the best in class and natural ingredients to achieve desired results.
Fast Lean Pro is a herbal supplement that tricks your brain into imagining that you’re fasting and helps you maintain a healthy weight no matter when or what you eat.
Introducing Claritox Pro, a natural supplement designed to help you maintain your balance and prevent dizziness.
SightCare works by targeting the newly discovered root cause of vision impairment. According to research studies carried out by great universities and research centers, this root cause is a decrease in the antioxidant levels in the body.
GlucoTru Diabetes Supplement is a natural blend of various natural components.
Eye Fortin is a strong vision-supporting formula that supports healthy eyes and strong eyesight.
http://claritin.icu/# ventolin 108 mcg
paxlovid generic: cheap paxlovid online – Paxlovid buy online
paxlovid buy http://paxlovid.club/# paxlovid india
Healthy Nails
FitSpresso is a special supplement that makes it easier for you to lose weight. It has natural ingredients that help your body burn fat better.
Nervogen Pro is a dietary formula that contains 100% natural ingredients. The powerful blend of ingredients claims to support a healthy nervous system. Each capsule includes herbs and antioxidants that protect the nerve against damage and nourishes the nerves with the required nutrients. Order Your Nervogen Pro™ Now!
Buy neurodrine memory supplement (Official). The simplest way to maintain a steel trap memory
https://paxlovid.club/# paxlovid for sale
NeuroPure is a breakthrough dietary formula designed to alleviate neuropathy, a condition that affects a significant number of individuals with diabetes.
NeuroRise™ is one of the popular and best tinnitus supplements that help you experience 360-degree hearing
neurontin cost generic: buy gabapentin – neurontin price in india
http://gabapentin.life/# neurontin 900 mg
Buy ProDentim Official Website with 50% off Free Fast Shipping
Buy Protoflow 50% off USA (Official). Protoflow is a natural and effective leader in prostate health supplements
ventolin otc uk: ventolin without prescription – ventolin for sale online
SeroLean follows an AM-PM daily routine that boosts serotonin levels. Modulating the synthesis of serotonin aids in mood enhancement
VidaCalm is an herbal supplement that claims to permanently silence tinnitus.
Alpha Tonic daily testosterone booster for energy and performance. Convenient powder form ensures easy blending into drinks for optimal absorption.
Neurozoom is one of the best supplements out on the market for supporting your brain health and, more specifically, memory functions.
http://wellbutrin.rest/# wellbutrin pills
ProstateFlux™ is a natural supplement designed by experts to protect prostate health without interfering with other body functions.
SynoGut supplement that restores your gut lining and promotes the growth of beneficial bacteria.
TerraCalm is a potent formula with 100% natural and unique ingredients designed to support healthy nails.
Pineal XT™ is a dietary supplement crafted from entirely organic ingredients, ensuring a natural formulation.
SonoVive™ is a 100% natural hearing supplement by Sam Olsen made with powerful ingredients that help heal tinnitus problems and restore your hearing.
TonicGreens is a revolutionary product that can transform your health and strengthen your immune system!
Tropislim, is an all-natural dietary supplement. It promotes healthy weight loss through a proprietary blend of tropical plants and nutrients.
buy paxlovid online: Paxlovid without a doctor – paxlovid cost without insurance
Aw, this was a very nice post. In concept I want to put in writing like this additionally – taking time and actual effort to make an excellent article… but what can I say… I procrastinate alot and certainly not seem to get something done.
http://wellbutrin.rest/# cost of wellbutrin 75mg
farmacia online più conveniente: farmacia online migliore – farmacie online sicure
farmacia online miglior prezzo Farmacie a roma che vendono cialis senza ricetta farmacie on line spedizione gratuita
dove acquistare viagra in modo sicuro: viagra senza ricetta – pillole per erezioni fortissime
http://sildenafilit.bid/# viagra cosa serve
farmacia online più conveniente: avanafil generico – farmacia online miglior prezzo
I do like the way you have presented this specific problem and it really does give us a lot of fodder for consideration. Nevertheless, through just what I have personally seen, I just simply wish when other opinions stack on that individuals stay on issue and not start on a tirade involving the news of the day. All the same, thank you for this superb point and although I can not really go along with this in totality, I regard the perspective.
alternativa al viagra senza ricetta in farmacia: viagra prezzo farmacia – alternativa al viagra senza ricetta in farmacia
farmacie online autorizzate elenco: avanafil generico prezzo – farmacie online sicure
BioVanish is a supplement from WellMe that helps consumers improve their weight loss by transitioning to ketosis.
Joint Genesis is a supplement from BioDynamix that helps consumers to improve their joint health to reduce pain.
GlucoBerry is a unique supplement that offers an easy and effective way to support balanced blood sugar levels.
farmacie online autorizzate elenco: Farmacie a milano che vendono cialis senza ricetta – comprare farmaci online all’estero
viagra cosa serve viagra prezzo farmacia viagra acquisto in contrassegno in italia
cerco viagra a buon prezzo: viagra consegna in 24 ore pagamento alla consegna – viagra generico in farmacia costo
cialis farmacia senza ricetta: viagra generico – farmacia senza ricetta recensioni
comprare farmaci online con ricetta: farmacia online spedizione gratuita – farmacia online senza ricetta
farmacia online più conveniente: cialis generico consegna 48 ore – farmacia online migliore
farmacia online: farmacia online migliore – farmacia online
Cortexi is a natural hearing support aid that has been used by thousands of people around the globe.
https://farmaciait.pro/# migliori farmacie online 2023
farmacia online migliore: kamagra gel – farmacia online
you’re in point of fact a excellent webmaster. The site loading speed is amazing. It kind of feels that you are doing any unique trick. In addition, The contents are masterpiece. you’ve performed a wonderful task in this subject!
comprare farmaci online con ricetta: avanafil – farmacia online miglior prezzo
viagra originale in 24 ore contrassegno: viagra online spedizione gratuita – viagra online in 2 giorni
farmacie online sicure: avanafil spedra – п»їfarmacia online migliore
comprare farmaci online all’estero: comprare avanafil senza ricetta – acquistare farmaci senza ricetta
SharpEar™ is a 100% natural ear care supplement created by Sam Olsen that helps to fix hearing loss
farmacie online affidabili: Tadalafil generico – farmacia online migliore
Thanks for this howling post, I am glad I discovered this internet site on yahoo.
Hey, you used to write great, but the last few posts have been kinda boring… I miss your tremendous writings. Past several posts are just a little out of track! come on!
acquistare farmaci senza ricetta: comprare avanafil senza ricetta – farmacia online senza ricetta
farmacie online sicure: kamagra oral jelly consegna 24 ore – farmacie online sicure
Thanks for sharing superb informations. Your web-site is very cool. I’m impressed by the details that you’ve on this web site. It reveals how nicely you understand this subject. Bookmarked this web page, will come back for extra articles. You, my friend, ROCK! I found simply the information I already searched all over the place and simply could not come across. What a great web-site.
viagra generico in farmacia costo: viagra prezzo – cerco viagra a buon prezzo
farmacia online senza ricetta: Farmacie che vendono Cialis senza ricetta – farmacia online migliore
farmacia online più conveniente: kamagra oral jelly consegna 24 ore – farmacie online autorizzate elenco
farmacia online: kamagra gel prezzo – top farmacia online
viagra subito: viagra online siti sicuri – viagra ordine telefonico
https://avanafilit.icu/# п»їfarmacia online migliore
dove acquistare viagra in modo sicuro: viagra prezzo – viagra generico in farmacia costo
farmacia online miglior prezzo kamagra gold farmacie online affidabili
farmacia online miglior prezzo: farmacia online miglior prezzo – comprare farmaci online con ricetta
I’ve recently started a web site, the info you provide on this website has helped me greatly. Thanks for all of your time & work.
viagra subito: viagra online siti sicuri – viagra originale recensioni
You must participate in a contest for probably the greatest blogs on the web. I will recommend this website!
Respect to article author, some excellent selective information.
farmacia online senza ricetta: kamagra gel prezzo – farmaci senza ricetta elenco
farmacie online autorizzate elenco: farmacia online – farmacia online più conveniente
Spot on with this write-up, I truly think this website wants way more consideration. I’ll in all probability be again to learn far more, thanks for that info.
farmacia online migliore: farmacia online migliore – acquisto farmaci con ricetta
Good info. Lucky me I reach on your website by accident, I bookmarked it.
http://avanafilit.icu/# farmacie online autorizzate elenco
migliori farmacie online 2023 kamagra gold farmacie online sicure
farmacia online migliore: kamagra gold – farmacia online miglior prezzo
http://vardenafilo.icu/# farmacia online madrid
I have learn a few excellent stuff here. Definitely value bookmarking for revisiting. I wonder how so much attempt you set to create this kind of magnificent informative web site.
farmacia online envГo gratis: Precio Levitra En Farmacia – farmacias online baratas
https://kamagraes.site/# farmacia barata
I see something genuinely special in this site.
https://sildenafilo.store/# п»їViagra online cerca de Madrid
https://vardenafilo.icu/# farmacia online
http://kamagraes.site/# farmacia envÃos internacionales
farmacia barata farmacia online barata farmacia envГos internacionales
https://tadalafilo.pro/# farmacia 24h
farmacia envГos internacionales: farmacia envio gratis – farmacias online seguras
http://farmacia.best/# farmacia 24h
https://vardenafilo.icu/# farmacias online seguras en espaГ±a
https://kamagraes.site/# farmacias baratas online envÃo gratis
https://kamagraes.site/# farmacia online
http://tadalafilo.pro/# farmacias online seguras en españa
п»їfarmacia online comprar cialis online seguro farmacia 24h
https://sildenafilo.store/# sildenafilo precio farmacia
farmacia online internacional: Levitra precio – farmacia online envГo gratis
http://farmacia.best/# farmacia online 24 horas
http://farmacia.best/# farmacias online seguras en espaГ±a
I wanted to thank you for this great read!! I definitely enjoying every little bit of it I have you bookmarked to check out new stuff you post…
What i do not understood is if truth be told how you’re not really a lot more well-favored than you may be right now. You’re so intelligent. You realize thus considerably relating to this subject, produced me personally imagine it from so many various angles. Its like men and women aren’t involved unless it’s something to do with Woman gaga! Your individual stuffs nice. At all times deal with it up!
farmacias online seguras en espaГ±a farmacia 24 horas farmacia online madrid
sildenafil 100mg genГ©rico: viagra para hombre venta libre – comprar viagra online en andorra
https://sildenafilo.store/# viagra para hombre venta libre
https://kamagraes.site/# farmacia online
https://tadalafilo.pro/# farmacia online internacional
https://sildenafilo.store/# venta de viagra a domicilio
http://vardenafilo.icu/# farmacia online
https://vardenafilo.icu/# farmacia envÃos internacionales
farmacia online barata: vardenafilo – farmacias online seguras
farmacia online internacional vardenafilo sin receta farmacias baratas online envГo gratis
http://tadalafilo.pro/# farmacia online barata
https://tadalafilo.pro/# farmacias online baratas
http://farmacia.best/# farmacia online barata
https://kamagraes.site/# farmacias online seguras en españa
https://farmacia.best/# farmacias online seguras
https://sildenafilo.store/# comprar sildenafilo cinfa 100 mg españa
п»їfarmacia online: Levitra precio – farmacia online envГo gratis
http://vardenafilo.icu/# farmacias online seguras en españa
п»їViagra online cerca de Madrid comprar viagra contrareembolso 48 horas sildenafilo 50 mg precio sin receta
https://tadalafilo.pro/# farmacia online madrid
https://vardenafilo.icu/# farmacia online internacional
https://kamagraes.site/# farmacias online seguras en españa
sildenafilo 100mg precio espaГ±a: comprar viagra contrareembolso 48 horas – venta de viagra a domicilio
Hmm it seems like your site ate my first comment (it was extremely long) so I guess I’ll just sum it up what I had written and say, I’m thoroughly enjoying your blog. I too am an aspiring blog writer but I’m still new to everything. Do you have any helpful hints for inexperienced blog writers? I’d certainly appreciate it.
https://kamagraes.site/# farmacias online seguras
https://kamagraes.site/# farmacia online internacional
farmacia online internacional Comprar Levitra Sin Receta En Espana farmacia online internacional
https://farmacia.best/# farmacia online madrid
http://kamagraes.site/# farmacia online
What¦s Happening i’m new to this, I stumbled upon this I’ve found It absolutely helpful and it has helped me out loads. I hope to contribute & aid different customers like its aided me. Great job.
http://vardenafilo.icu/# farmacias online baratas
https://tadalafilo.pro/# farmacias online seguras
http://kamagraes.site/# farmacia online madrid
https://vardenafilo.icu/# farmacia envГos internacionales
https://sildenafilo.store/# sildenafilo 50 mg precio sin receta
farmacias online seguras en espaГ±a: farmacia online envio gratis valencia – farmacia online madrid
farmacia online barata precio cialis en farmacia con receta farmacia online internacional
https://sildenafilo.store/# comprar viagra online en andorra
https://tadalafilo.pro/# farmacias online seguras en españa
http://pharmacieenligne.guru/# Pharmacie en ligne livraison rapide
farmacias online seguras en espaГ±a: kamagra – farmacia online madrid
http://cialissansordonnance.pro/# Pharmacie en ligne livraison 24h
Viagra homme prix en pharmacie sans ordonnance: Viagra sans ordonnance 24h – Viagra sans ordonnance 24h suisse
I have been exploring for a little bit for any high quality articles or weblog posts on this kind of space . Exploring in Yahoo I ultimately stumbled upon this website. Reading this info So i¦m satisfied to exhibit that I’ve a very excellent uncanny feeling I found out just what I needed. I most indisputably will make sure to do not disregard this site and provides it a glance on a continuing basis.
https://kamagrafr.icu/# Pharmacie en ligne livraison gratuite
Acheter mГ©dicaments sans ordonnance sur internet tadalafil Pharmacie en ligne France
https://levitrafr.life/# Pharmacie en ligne livraison gratuite
https://pharmacieenligne.guru/# acheter médicaments à l’étranger
farmacia 24h: farmacia envio gratis – farmacia online 24 horas
pharmacie ouverte: Medicaments en ligne livres en 24h – Pharmacies en ligne certifiГ©es
http://viagrasansordonnance.store/# Sildénafil Teva 100 mg acheter
https://kamagrafr.icu/# acheter médicaments à l’étranger
Great web site. A lot of useful info here. I¦m sending it to some pals ans additionally sharing in delicious. And of course, thank you to your sweat!
https://levitrafr.life/# Pharmacie en ligne pas cher
Pharmacie en ligne pas cher pharmacie en ligne sans ordonnance Pharmacie en ligne livraison gratuite
https://levitrafr.life/# Pharmacie en ligne livraison 24h
https://viagrasansordonnance.store/# Viagra femme sans ordonnance 24h
Pharmacie en ligne livraison 24h: tadalafil – Pharmacie en ligne sans ordonnance
https://levitrafr.life/# pharmacie ouverte 24/24
https://viagrasansordonnance.store/# Sildénafil 100 mg prix en pharmacie en France
https://pharmacieenligne.guru/# acheter médicaments à l’étranger
Pharmacie en ligne sans ordonnance acheter kamagra site fiable Pharmacies en ligne certifiГ©es
http://viagrasansordonnance.store/# Viagra homme prix en pharmacie sans ordonnance
viagra para hombre precio farmacias: viagra entrega inmediata – comprar viagra online en andorra
http://cialissansordonnance.pro/# pharmacie ouverte 24/24
https://kamagrafr.icu/# Acheter médicaments sans ordonnance sur internet
Viagra pas cher livraison rapide france: Acheter du Viagra sans ordonnance – Quand une femme prend du Viagra homme
http://cialissansordonnance.pro/# Pharmacie en ligne livraison rapide
Thank you so much for giving everyone such a breathtaking chance to read in detail from this web site. It’s always very cool and packed with fun for me and my office peers to search the blog at the least thrice per week to learn the newest things you will have. And of course, we’re actually impressed with your breathtaking creative concepts served by you. Selected 2 facts in this post are in reality the most effective we have all ever had.
I really like your writing style, wonderful info, appreciate it for putting up :D. “Freedom is the emancipation from the arbitrary rule of other men.” by Mortimer Adler.
https://viagrasansordonnance.store/# Viagra pas cher livraison rapide france
farmacia online envГo gratis: comprar kamagra en espana – farmacias online seguras
https://levitrafr.life/# Pharmacie en ligne France
I discovered your blog site on google and check a few of your early posts. Continue to keep up the very good operate. I just additional up your RSS feed to my MSN News Reader. Seeking forward to reading more from you later on!…
http://pharmacieenligne.guru/# pharmacie en ligne
Simply wanna comment on few general things, The website layout is perfect, the subject matter is very fantastic. “The enemy is anybody who’s going to get you killed, no matter which side he’s on.” by Joseph Heller.
Sildenafil rezeptfrei in welchem Land Viagra verschreibungspflichtig Viagra Preis Schwarzmarkt
http://apotheke.company/# versandapotheke versandkostenfrei
https://apotheke.company/# versandapotheke deutschland
Viagra Alternative rezeptfrei viagra ohne rezept Billig Viagra bestellen ohne Rezept
of course like your web site but you need to check the spelling on several of your posts. Several of them are rife with spelling issues and I in finding it very troublesome to inform the reality then again I?¦ll definitely come again again.
Nice post. I learn something more challenging on different blogs everyday. It will always be stimulating to read content from other writers and practice a little something from their store. I’d prefer to use some with the content on my blog whether you don’t mind. Natually I’ll give you a link on your web blog. Thanks for sharing.
http://apotheke.company/# versandapotheke
https://viagrakaufen.store/# Sildenafil kaufen online
online apotheke preisvergleich kamagra jelly kaufen deutschland versandapotheke versandkostenfrei
Great – I should definitely pronounce, impressed with your web site. I had no trouble navigating through all tabs as well as related info ended up being truly simple to do to access. I recently found what I hoped for before you know it at all. Reasonably unusual. Is likely to appreciate it for those who add forums or something, website theme . a tones way for your customer to communicate. Excellent task.
Saved as a favorite, I really like your blog!
Rattling informative and great anatomical structure of written content, now that’s user pleasant (:.
https://apotheke.company/# online apotheke preisvergleich
https://potenzmittel.men/# versandapotheke
This is very interesting, You are a very skilled blogger. I’ve joined your feed and look forward to seeking more of your great post. Also, I’ve shared your website in my social networks!
fantastic post, very informative. I wonder why the other specialists of this sector don’t notice this. You should continue your writing. I am sure, you’ve a huge readers’ base already!
Viagra Preis Schwarzmarkt viagra generika Sildenafil rezeptfrei in welchem Land
Your style is so unique compared to many other people. Thank you for publishing when you have the opportunity,Guess I will just make this bookmarked.2
http://cialiskaufen.pro/# online apotheke versandkostenfrei
We’re a group of volunteers and opening a brand new scheme in our community. Your web site provided us with helpful info to work on. You have done a formidable job and our whole group can be thankful to you.
versandapotheke versandkostenfrei: online apotheke rezeptfrei – online-apotheken
versandapotheke deutschland kamagra online bestellen online apotheke gГјnstig
I got what you intend,saved to my bookmarks, very nice website .
mexico pharmacy reputable mexican pharmacies online mexican online pharmacies prescription drugs
mexico pharmacies prescription drugs medication from mexico pharmacy mexico drug stores pharmacies
pharmacies in mexico that ship to usa mexican online pharmacies prescription drugs mexico pharmacy
https://mexicanpharmacy.cheap/# mexican rx online
pharmacies in mexico that ship to usa reputable mexican pharmacies online mexican pharmaceuticals online
Hello, you used to write great, but the last few posts have been kinda boring… I miss your tremendous writings. Past few posts are just a bit out of track! come on!
buying from online mexican pharmacy mexico drug stores pharmacies mexican mail order pharmacies
pharmacies in mexico that ship to usa purple pharmacy mexico price list buying prescription drugs in mexico
Very interesting information!Perfect just what I was searching for! “All the really good ideas I ever had came to me while I was milking a cow.” by Grant Wood.
http://mexicanpharmacy.cheap/# mexico drug stores pharmacies
mexico pharmacies prescription drugs mexican pharmaceuticals online mexican border pharmacies shipping to usa
mexican border pharmacies shipping to usa buying prescription drugs in mexico best online pharmacies in mexico
I keep listening to the news update lecture about getting boundless online grant applications so I have been looking around for the most excellent site to get one. Could you advise me please, where could i acquire some?
buying prescription drugs in mexico online purple pharmacy mexico price list medication from mexico pharmacy
http://mexicanpharmacy.cheap/# mexican mail order pharmacies
Oh my goodness! an incredible article dude. Thank you Nevertheless I’m experiencing situation with ur rss . Don’t know why Unable to subscribe to it. Is there anybody getting similar rss drawback? Anyone who knows kindly respond. Thnkx
https://mexicanpharmacy.cheap/# mexican border pharmacies shipping to usa
reputable mexican pharmacies online reputable mexican pharmacies online mexican border pharmacies shipping to usa
http://mexicanpharmacy.cheap/# mexican border pharmacies shipping to usa
reputable mexican pharmacies online mexican mail order pharmacies purple pharmacy mexico price list
My wife and i have been so delighted that Peter managed to finish up his web research while using the ideas he gained out of your weblog. It is now and again perplexing to just continually be giving out concepts which other folks have been trying to sell. And now we figure out we have got the blog owner to appreciate because of that. All the illustrations you have made, the easy blog navigation, the friendships you can make it possible to instill – it’s got many great, and it is facilitating our son in addition to our family imagine that this situation is entertaining, and that is seriously indispensable. Many thanks for all the pieces!
Boostaro increases blood flow to the reproductive organs, leading to stronger and more vibrant erections. It provides a powerful boost that can make you feel like you’ve unlocked the secret to firm erections
mexico pharmacies prescription drugs mexico pharmacies prescription drugs mexican drugstore online
I have been absent for some time, but now I remember why I used to love this website. Thank you, I’ll try and check back more often. How frequently you update your web site?
purple pharmacy mexico price list buying prescription drugs in mexico mexican rx online
mexican drugstore online buying prescription drugs in mexico online purple pharmacy mexico price list
http://mexicanpharmacy.cheap/# mexican border pharmacies shipping to usa
Prostadine™ is a revolutionary new prostate support supplement designed to protect, restore, and enhance male prostate health.
buying prescription drugs in mexico buying from online mexican pharmacy mexican pharmaceuticals online
Aizen Power is a dietary supplement for male enhancement
http://mexicanpharmacy.cheap/# mexico pharmacies prescription drugs
Neotonics is a dietary supplement that offers help in retaining glowing skin and maintaining gut health for its users. It is made of the most natural elements that mother nature can offer and also includes 500 million units of beneficial microbiome.
purple pharmacy mexico price list mexican pharmaceuticals online buying prescription drugs in mexico
EndoPeak is a male health supplement with a wide range of natural ingredients that improve blood circulation and vitality.
Glucotrust is one of the best supplements for managing blood sugar levels or managing healthy sugar metabolism.
buying prescription drugs in mexico mexican online pharmacies prescription drugs mexico drug stores pharmacies
EyeFortin is a natural vision support formula crafted with a blend of plant-based compounds and essential minerals. It aims to enhance vision clarity, focus, and moisture balance.
Support the health of your ears with 100% natural ingredients, finally being able to enjoy your favorite songs and movies
medicine in mexico pharmacies buying prescription drugs in mexico online mexican border pharmacies shipping to usa
GlucoBerry is a meticulously crafted supplement designed by doctors to support healthy blood sugar levels by harnessing the power of delphinidin—an essential compound.
Free Shiping If You Purchase Today!
mexican border pharmacies shipping to usa mexican rx online mexican mail order pharmacies
ProDentim is a nutritional dental health supplement that is formulated to reverse serious dental issues and to help maintain good dental health.
pharmacies in mexico that ship to usa medication from mexico pharmacy buying from online mexican pharmacy
mexican rx online best online pharmacies in mexico mexican drugstore online
best ed pill cure ed – erectile dysfunction medicines edpills.tech
male erection pills mens erection pills – ed pills online edpills.tech
Online medicine home delivery india online pharmacy best india pharmacy indiapharmacy.guru
canadian pharmacy india indian pharmacies safe – online pharmacy india indiapharmacy.guru
SonoVive™ is a completely natural hearing support formula made with powerful ingredients that help heal tinnitus problems and restore your hearing
BioFit™ is a Nutritional Supplement That Uses Probiotics To Help You Lose Weight
Hi my loved one! I wish to say that this post is awesome, great written and come with approximately all vital infos. I would like to see more posts like this .
http://indiapharmacy.pro/# india online pharmacy indiapharmacy.pro
reputable indian online pharmacy Online medicine order – buy medicines online in india indiapharmacy.guru
Dentitox Pro is a liquid dietary solution created as a serum to support healthy gums and teeth. Dentitox Pro formula is made in the best natural way with unique, powerful botanical ingredients that can support healthy teeth.
The ingredients of Endo Pump Male Enhancement are all-natural and safe to use.
Gorilla Flow is a non-toxic supplement that was developed by experts to boost prostate health for men.
canadian pharmacy meds canadian pharmacy uk delivery canadian pharmacy 365 canadiandrugs.tech
ed meds online natural remedies for ed – best ed drug edpills.tech
GlucoCare is a natural and safe supplement for blood sugar support and weight management. It fixes your metabolism and detoxifies your body.
Nervogen Pro, A Cutting-Edge Supplement Dedicated To Enhancing Nerve Health And Providing Natural Relief From Discomfort. Our Mission Is To Empower You To Lead A Life Free From The Limitations Of Nerve-Related Challenges. With A Focus On Premium Ingredients And Scientific Expertise.
Neurodrine is a fantastic dietary supplement that protects your mind and improves memory performance. It can help you improve your focus and concentration.
InchaGrow is an advanced male enhancement supplement. The Formula is Easy to Take Each Day, and it Only Uses. Natural Ingredients to Get the Desired Effect
HoneyBurn is a 100% natural honey mixture formula that can support both your digestive health and fat-burning mechanism. Since it is formulated using 11 natural plant ingredients, it is clinically proven to be safe and free of toxins, chemicals, or additives.
GlucoFlush™ is an all-natural supplement that uses potent ingredients to control your blood sugar.
Online medicine order Online medicine order – indianpharmacy com indiapharmacy.guru
legit canadian pharmacy online buying drugs from canada safe reliable canadian pharmacy canadiandrugs.tech
SynoGut is a natural dietary supplement specifically formulated to support digestive function and promote a healthy gut microbiome.
Amiclear is a dietary supplement designed to support healthy blood sugar levels and assist with glucose metabolism. It contains eight proprietary blends of ingredients that have been clinically proven to be effective.
https://canadiandrugs.tech/# pharmacy canadian superstore canadiandrugs.tech
Tải Hit Club iOS
Tải Hit Club iOSHIT CLUBHit Club đã sáng tạo ra một giao diện game đẹp mắt và hoàn thiện, lấy cảm hứng từ các cổng casino trực tuyến chất lượng từ cổ điển đến hiện đại. Game mang lại sự cân bằng và sự kết hợp hài hòa giữa phong cách sống động của sòng bạc Las Vegas và phong cách chân thực. Tất cả các trò chơi đều được bố trí tinh tế và hấp dẫn với cách bố trí game khoa học và logic giúp cho người chơi có được trải nghiệm chơi game tốt nhất.
Hit Club – Cổng Game Đổi Thưởng
Trên trang chủ của Hit Club, người chơi dễ dàng tìm thấy các game bài, tính năng hỗ trợ và các thao tác để rút/nạp tiền cùng với cổng trò chuyện trực tiếp để được tư vấn. Giao diện game mang lại cho người chơi cảm giác chân thật và thoải mái nhất, giúp người chơi không bị mỏi mắt khi chơi trong thời gian dài.
Hướng Dẫn Tải Game Hit Club
Bạn có thể trải nghiệm Hit Club với 2 phiên bản: Hit Club APK cho thiết bị Android và Hit Club iOS cho thiết bị như iPhone, iPad.
Tải ứng dụng game:
Click nút tải ứng dụng game ở trên (phiên bản APK/Android hoặc iOS tùy theo thiết bị của bạn).
Chờ cho quá trình tải xuống hoàn tất.
Cài đặt ứng dụng:
Khi quá trình tải xuống hoàn tất, mở tệp APK hoặc iOS và cài đặt ứng dụng trên thiết bị của bạn.
Bắt đầu trải nghiệm:
Mở ứng dụng và bắt đầu trải nghiệm Hit Club.
Với Hit Club, bạn sẽ khám phá thế giới game đỉnh cao với giao diện đẹp mắt và trải nghiệm chơi game tuyệt vời. Hãy tải ngay để tham gia vào cuộc phiêu lưu casino độc đáo và đầy hứng khởi!
mail order pharmacy india buy medicines online in india – best india pharmacy indiapharmacy.guru
https://mexicanpharmacy.company/# mexican pharmacy mexicanpharmacy.company
Would love to perpetually get updated outstanding weblog! .
canadian pharmacy king my canadian pharmacy online canadian pharmacy review canadiandrugs.tech
https://edpills.tech/# top erection pills edpills.tech
top online pharmacy india india online pharmacy – indian pharmacy paypal indiapharmacy.guru
Metabo Flex is a nutritional formula that enhances metabolic flexibility by awakening the calorie-burning switch in the body. The supplement is designed to target the underlying causes of stubborn weight gain utilizing a special “miracle plant” from Cambodia that can melt fat 24/7.
GlucoFlush Supplement is an all-new blood sugar-lowering formula. It is a dietary supplement based on the Mayan cleansing routine that consists of natural ingredients and nutrients.
SynoGut is an all-natural dietary supplement that is designed to support the health of your digestive system, keeping you energized and active.
Manufactured in an FDA-certified facility in the USA, EndoPump is pure, safe, and free from negative side effects. With its strict production standards and natural ingredients, EndoPump is a trusted choice for men looking to improve their sexual performance.
Gorilla Flow is a non-toxic supplement that was developed by experts to boost prostate health for men. It’s a blend of all-natural nutrients, including Pumpkin Seed Extract Stinging Nettle Extract, Gorilla Cherry and Saw Palmetto, Boron, and Lycopene.
Nervogen Pro is a cutting-edge dietary supplement that takes a holistic approach to nerve health. It is meticulously crafted with a precise selection of natural ingredients known for their beneficial effects on the nervous system. By addressing the root causes of nerve discomfort, Nervogen Pro aims to provide lasting relief and support for overall nerve function.
While Inchagrow is marketed as a dietary supplement, it is important to note that dietary supplements are regulated by the FDA. This means that their safety and effectiveness, and there is 60 money back guarantee that Inchagrow will work for everyone.
Herpagreens is a dietary supplement formulated to combat symptoms of herpes by providing the body with high levels of super antioxidants, vitamins
SonoVive is an all-natural supplement made to address the root cause of tinnitus and other inflammatory effects on the brain and promises to reduce tinnitus, improve hearing, and provide peace of mind. SonoVive is is a scientifically verified 10-second hack that allows users to hear crystal-clear at maximum volume. The 100% natural mix recipe improves the ear-brain link with eight natural ingredients. The treatment consists of easy-to-use pills that can be added to one’s daily routine to improve hearing health, reduce tinnitus, and maintain a sharp mind and razor-sharp focus.
Unquestionably consider that that you stated. Your favourite justification appeared to be at the internet the simplest thing to have in mind of. I say to you, I definitely get annoyed at the same time as other folks consider issues that they plainly don’t recognise about. You controlled to hit the nail upon the highest and outlined out the entire thing without having side effect , people could take a signal. Will probably be back to get more. Thanks
TerraCalm is an antifungal mineral clay that may support the health of your toenails. It is for those who struggle with brittle, weak, and discoloured nails. It has a unique blend of natural ingredients that may work to nourish and strengthen your toenails.
http://edpills.tech/# medication for ed edpills.tech
http://edpills.tech/# best over the counter ed pills edpills.tech
canadian pharmacy my canadian pharmacy rx my canadian pharmacy canadiandrugs.tech
https://edpills.tech/# top ed pills edpills.tech
Как включить аппаратную виртуализацию
Абузоустойчивый серверов для Хрумера и GSA AMSTERDAM!!!
Оптимальная Настройка: Включение Аппаратной Виртуализации
При обсуждении виртуальных серверов (VPS/VDS) и дедикатед серверов, важно также уделить внимание оптимальной настройке, включая аппаратную виртуализацию. Этот важный аспект может значительно повлиять на производительность вашего сервера.
Высокоскоростной Интернет: До 1000 Мбит/с
https://canadiandrugs.tech/# canadian pharmacy king reviews canadiandrugs.tech
canadian pharmacy world canada cloud pharmacy – trustworthy canadian pharmacy canadiandrugs.tech
http://indiapharmacy.pro/# indian pharmacy indiapharmacy.pro
medicine erectile dysfunction best over the counter ed pills male erection pills edpills.tech
my canadian pharmacy reviews best canadian pharmacy online – legit canadian pharmacy canadiandrugs.tech
http://indiapharmacy.guru/# best online pharmacy india indiapharmacy.guru
オンラインカジノとオンラインギャンブルの現代的展開
オンラインカジノの世界は、技術の進歩と共に急速に進化しています。これらのプラットフォームは、従来の実際のカジノの体験をデジタル空間に移し、プレイヤーに新しい形式の娯楽を提供しています。オンラインカジノは、スロットマシン、ポーカー、ブラックジャック、ルーレットなど、さまざまなゲームを提供しており、実際のカジノの興奮を維持しながら、アクセスの容易さと利便性を提供します。
一方で、オンラインギャンブルは、より広範な概念であり、スポーツベッティング、宝くじ、バーチャルスポーツ、そしてオンラインカジノゲームまでを含んでいます。インターネットとモバイルテクノロジーの普及により、オンラインギャンブルは世界中で大きな人気を博しています。オンラインプラットフォームは、伝統的な賭博施設に比べて、より多様なゲーム選択、便利なアクセス、そしてしばしば魅力的なボーナスやプロモーションを提供しています。
安全性と規制
オンラインカジノとオンラインギャンブルの世界では、安全性と規制が非常に重要です。多くの国々では、オンラインギャンブルを規制する法律があり、安全なプレイ環境を確保するためのライセンスシステムを設けています。これにより、不正行為や詐欺からプレイヤーを守るとともに、責任ある賭博の促進が図られています。
技術の進歩
最新のテクノロジーは、オンラインカジノとオンラインギャンブルの体験を一層豊かにしています。例えば、仮想現実(VR)技術の使用は、プレイヤーに没入型のギャンブル体験を提供し、実際のカジノにいるかのような感覚を生み出しています。また、ブロックチェーン技術の導入は、より透明で安全な取引を可能にし、プレイヤーの信頼を高めています。
未来への展望
オンラインカジノとオンラインギャンブルは、今後も技術の進歩とともに進化し続けるでしょう。人工知能(AI)の更なる統合、モバイル技術の発展、さらには新しいゲームの創造により、この分野は引き続き成長し、世界中のプレイヤーに新しい娯楽の形を提供し続けることでしょう。
この記事では、オンラインカジノとオンラインギャンブルの現状、安全性、技術の影響、そして将来の展望に焦点を当てています。この分野は、技術革新によって絶えず変化し続ける魅力的な領域です。
cheap erectile dysfunction pill best male ed pills – new ed pills edpills.tech
GlucoTrust is a revolutionary blood sugar support solution that eliminates the underlying causes of type 2 diabetes and associated health risks.
where to buy clomid without insurance where can i get clomid pill can i order cheap clomid without rx
https://prednisone.bid/# iv prednisone
http://prednisone.bid/# prednisone tablet 100 mg
prednisone 20 mg prednisone online for sale prednisone 250 mg
https://clomid.site/# get clomid without a prescription
https://prednisone.bid/# prednisone over the counter australia
prednisone 10mg prices prednisone 10mg tabs prednisone uk buy
buy amoxicillin 250mg: amoxicillin capsules 250mg – ampicillin amoxicillin
cipro 500mg best prices where can i buy cipro online buy cipro online usa
I’d always want to be update on new content on this web site, saved to my bookmarks! .
http://amoxil.icu/# amoxicillin 500 mg for sale
http://amoxil.icu/# amoxicillin 500 tablet
buy cipro online without prescription buy cipro without rx cipro pharmacy
http://paxlovid.win/# paxlovid india
canadian pharmacy amoxicillin amoxicillin online without prescription amoxicillin without rx
where can i buy amoxicillin over the counter uk: amoxicillin brand name – amoxicillin generic
prednisone medication prednisone 30 prednisone brand name us
http://ciprofloxacin.life/# buy ciprofloxacin over the counter
where to buy amoxicillin generic for amoxicillin buy amoxicillin 500mg capsules uk
ciprofloxacin generic price: п»їcipro generic – buy ciprofloxacin over the counter
I haven¦t checked in here for a while since I thought it was getting boring, but the last few posts are good quality so I guess I¦ll add you back to my daily bloglist. You deserve it my friend 🙂
http://clomid.site/# where can i buy clomid no prescription
I’m still learning from you, while I’m trying to achieve my goals. I absolutely liked reading all that is written on your site.Keep the information coming. I enjoyed it!
Buy discount supplements, vitamins, health supplements, probiotic supplements. Save on top vitamin and supplement brands.
Cortexi is an effective hearing health support formula that has gained positive user feedback for its ability to improve hearing ability and memory. This supplement contains natural ingredients and has undergone evaluation to ensure its efficacy and safety. Manufactured in an FDA-registered and GMP-certified facility, Cortexi promotes healthy hearing, enhances mental acuity, and sharpens memory.
Абузоустойчивый сервер для работы с Хрумером, GSA и всевозможными скриптами!
Есть дополнительная системах скидок, читайте описание в разделе оплата
Виртуальные сервера (VPS/VDS) и Дедик Сервер: Оптимальное Решение для Вашего Проекта
В мире современных вычислений виртуальные сервера (VPS/VDS) и дедик сервера становятся ключевыми элементами успешного бизнеса и онлайн-проектов. Выбор оптимальной операционной системы и типа сервера являются решающими шагами в создании надежной и эффективной инфраструктуры. Наши VPS/VDS серверы Windows и Linux, доступные от 13 рублей, а также дедик серверы, предлагают целый ряд преимуществ, делая их неотъемлемыми инструментами для развития вашего проекта.
While improving eyesight isn’t often the goal of consumers who wear their glasses religiously, it doesn’t mean they’re stuck where they are.
Sight Care is a daily supplement proven in clinical trials and conclusive science to improve vision by nourishing the body from within. The Sight Care formula claims to reverse issues in eyesight, and every ingredient is completely natural.
What’s Happening i’m new to this, I stumbled upon this I’ve found It positively helpful and it has aided me out loads. I hope to contribute & aid other users like its aided me. Good job.
I have read several good stuff here. Definitely value bookmarking for revisiting. I wonder how a lot attempt you set to make this type of fantastic informative site.
I like this weblog its a master peace ! Glad I detected this on google .
There is evidently a lot to identify about this. I consider you made certain good points in features also.
民意調查
My spouse and I stumbled over here by a different web page and thought I might as well check things out. I like what I see so now i am following you. Look forward to looking at your web page repeatedly.
Posta Kodu
https://doxycyclinebestprice.pro/# cheap doxycycline online
doxycycline medication doxycycline how to buy doxycycline online
zithromax 500mg over the counter: buy zithromax no prescription – zithromax 250 mg pill
https://cytotec.icu/# buy misoprostol over the counter
https://doxycyclinebestprice.pro/# doxycycline hyc 100mg
lisinopril buy in canada: buy lisinopril online uk – lisinopril 500 mg
lisinopril from mexico: lisinopril online canadian pharmacy – lisinopril 420 1g
總統民調
Nice post. I learn something more challenging on different blogs everyday. It will always be stimulating to read content from other writers and practice a little something from their store. I’d prefer to use some with the content on my blog whether you don’t mind. Natually I’ll give you a link on your web blog. Thanks for sharing.
https://nolvadex.fun/# tamoxifen mechanism of action
lisinopril pills 10 mg: lisinopril 20mg daily – cost of generic lisinopril
doxycycline: purchase doxycycline online – doxy 200
zithromax prescription zithromax generic price can you buy zithromax over the counter in australia
民調
民意調查是什麼?民調什麼意思?
民意調查又稱為輿論調查或民意測驗,簡稱民調。一般而言,民調是一種為了解公眾對某些政治、社會問題與政策的意見和態度,由專業民調公司或媒體進行的調查方法。
目的在於通過網路、電話、或書面等媒介,對大量樣本的問卷調查抽樣,利用統計學的抽樣理論來推斷較為客觀,且能較為精確地推論社會輿論或民意動向的一種方法。
以下是民意調查的一些基本特點和重要性:
抽樣:由於不可能向每一個人詢問意見,所以調查者會選擇一個代表性的樣本進行調查。這樣本的大小和抽樣方法都會影響調查的準確性和可靠性。
問卷設計:為了確保獲得可靠的結果,問卷必須經過精心設計,問題要清晰、不帶偏見,且易於理解。
數據分析:收集到的數據將被分析以得出結論。這可能包括計算百分比、平均值、標準差等,以及更複雜的統計分析。
多種用途:民意調查可以用於各種目的,包括政策制定、選舉預測、市場研究、社會科學研究等。
限制:雖然民意調查是一個有價值的工具,但它也有其限制。例如,樣本可能不完全代表目標人群,或者問卷的設計可能導致偏見。
影響決策:民意調查的結果常常被政府、企業和其他組織用來影響其決策。
透明度和誠實:為了維護調查的可信度,調查組織應該提供其調查方法、樣本大小、抽樣方法和可能的誤差範圍等詳細資訊。
民調是怎麼調查的?
民意調查(輿論調查)的意義是指為瞭解大多數民眾的看法、意見、利益與需求,以科學、系統與公正的資料,蒐集可以代表全部群眾(母體)的部分群眾(抽樣),設計問卷題目後,以人工或電腦詢問部分民眾對特定議題的看法與評價,利用抽樣出來部分民眾的意見與看法,來推論目前全部民眾的意見與看法,藉以衡量社會與政治的狀態。
以下是進行民調調查的基本步驟:
定義目標和目的:首先,調查者需要明確調查的目的。是要了解公眾對某個政策的看法?還是要評估某個政治候選人的支持率?
設計問卷:根據調查目的,研究者會設計一份問卷。問卷應該包含清晰、不帶偏見的問題,並避免導向性的語言。
選擇樣本:因為通常不可能調查所有人,所以會選擇一部分人作為代表。這部分人被稱為“樣本”。最理想的情況是使用隨機抽樣,以確保每個人都有被選中的機會。
收集數據:有多種方法可以收集數據,如面對面訪問、電話訪問、郵件調查或在線調查。
數據分析:一旦數據被收集,研究者會使用統計工具和技術進行分析,得出結論或洞見。
報告結果:分析完數據後,研究者會編寫報告或發布結果。報告通常會提供調查方法、樣本大小、誤差範圍和主要發現。
解釋誤差範圍:多數民調報告都會提供誤差範圍,例如“±3%”。這表示實際的結果有可能在報告結果的3%範圍內上下浮動。
民調調查的質量和可信度很大程度上取決於其設計和實施的方法。若是由專業和無偏見的組織進行,且使用科學的方法,那麼民調結果往往較為可靠。但即使是最高質量的民調也會有一定的誤差,因此解讀時應保持批判性思考。
為什麼要做民調?
民調提供了一種系統性的方式來了解大眾的意見、態度和信念。進行民調的原因多種多樣,以下是一些主要的動機:
政策制定和評估:政府和政策制定者進行民調,以了解公眾對某一議題或政策的看法。這有助於制定或調整政策,以反映大眾的需求和意見。
選舉和政治活動:政黨和候選人通常使用民調來評估自己在選舉中的地位,了解哪些議題對選民最重要,以及如何調整策略以吸引更多支持。
市場研究:企業和組織進行民調以了解消費者對產品、服務或品牌的態度,從而制定或調整市場策略。
社會科學研究:學者和研究者使用民調來了解人們的社會、文化和心理特征,以及其與行為的關係。
公眾與媒體的期望:民調提供了一種方式,使公眾、政府和企業得以了解社會的整體趨勢和態度。媒體也經常報導民調結果,提供公眾對當前議題的見解。
提供反饋和評估:無論是企業還是政府,都可以透過民調了解其表現、服務或政策的效果,並根據反饋進行改進。
預測和趨勢分析:民調可以幫助預測某些趨勢或行為的未來發展,如選舉結果、市場需求等。
教育和提高公眾意識:通過進行和公布民調,可以促使公眾對某一議題或問題有更深入的了解和討論。
民調可信嗎?
民意調查的結果數據隨處可見,尤其是政治性民調結果幾乎可說是天天在新聞上放送,對總統的滿意度下降了多少百分比,然而大家又信多少?
在景美市場的訪問中,我們了解到民眾對民調有一些普遍的觀點。大多數受訪者表示,他們對民調的可信度存有疑慮,主要原因是他們擔心政府可能會在調查中進行操控,以符合特定政治目標。
受訪者還提到,民意調查的結果通常不會對他們的投票意願產生影響。換句話說,他們的選擇通常受到更多因素的影響,例如候選人的政策立場和政府做事的認真與否,而不是單純依賴民調結果。
從訪問中我們可以得出的結論是,大多數民眾對民調持謹慎態度,並認為它們對他們的投票決策影響有限。
http://nolvadex.fun/# low dose tamoxifen
http://lisinoprilbestprice.store/# lisinopril cost uk
Misoprostol 200 mg buy online: buy cytotec online – п»їcytotec pills online
zithromax 500 mg: buy zithromax – zithromax 250 mg pill
http://lisinoprilbestprice.store/# lisinopril online without a prescription
zithromax tablets: can you buy zithromax over the counter in australia – zithromax 500 mg lowest price drugstore online
Wunderbarer Blog! Ich habe es beim Surfen auf Yahoo News gefunden. Haben Sie Vorschläge, wie Sie in Yahoo News gelistet werden? Ich versuche es schon eine Weile, aber ich scheine nie dort anzukommen! Danke
where to get doxycycline order doxycycline 100mg without prescription doxycycline without a prescription
VidaCalm is an all-natural blend of herbs and plant extracts that treat tinnitus and help you live a peaceful life.
Misoprostol 200 mg buy online: buy cytotec – buy cytotec over the counter
generic doxycycline: doxycycline generic – buy doxycycline monohydrate
https://zithromaxbestprice.icu/# generic zithromax 500mg india
https://nolvadex.fun/# tamoxifen reviews
民意調查是什麼?民調什麼意思?
民意調查又稱為輿論調查或民意測驗,簡稱民調。一般而言,民調是一種為了解公眾對某些政治、社會問題與政策的意見和態度,由專業民調公司或媒體進行的調查方法。
目的在於通過網路、電話、或書面等媒介,對大量樣本的問卷調查抽樣,利用統計學的抽樣理論來推斷較為客觀,且能較為精確地推論社會輿論或民意動向的一種方法。
以下是民意調查的一些基本特點和重要性:
抽樣:由於不可能向每一個人詢問意見,所以調查者會選擇一個代表性的樣本進行調查。這樣本的大小和抽樣方法都會影響調查的準確性和可靠性。
問卷設計:為了確保獲得可靠的結果,問卷必須經過精心設計,問題要清晰、不帶偏見,且易於理解。
數據分析:收集到的數據將被分析以得出結論。這可能包括計算百分比、平均值、標準差等,以及更複雜的統計分析。
多種用途:民意調查可以用於各種目的,包括政策制定、選舉預測、市場研究、社會科學研究等。
限制:雖然民意調查是一個有價值的工具,但它也有其限制。例如,樣本可能不完全代表目標人群,或者問卷的設計可能導致偏見。
影響決策:民意調查的結果常常被政府、企業和其他組織用來影響其決策。
透明度和誠實:為了維護調查的可信度,調查組織應該提供其調查方法、樣本大小、抽樣方法和可能的誤差範圍等詳細資訊。
民調是怎麼調查的?
民意調查(輿論調查)的意義是指為瞭解大多數民眾的看法、意見、利益與需求,以科學、系統與公正的資料,蒐集可以代表全部群眾(母體)的部分群眾(抽樣),設計問卷題目後,以人工或電腦詢問部分民眾對特定議題的看法與評價,利用抽樣出來部分民眾的意見與看法,來推論目前全部民眾的意見與看法,藉以衡量社會與政治的狀態。
以下是進行民調調查的基本步驟:
定義目標和目的:首先,調查者需要明確調查的目的。是要了解公眾對某個政策的看法?還是要評估某個政治候選人的支持率?
設計問卷:根據調查目的,研究者會設計一份問卷。問卷應該包含清晰、不帶偏見的問題,並避免導向性的語言。
選擇樣本:因為通常不可能調查所有人,所以會選擇一部分人作為代表。這部分人被稱為“樣本”。最理想的情況是使用隨機抽樣,以確保每個人都有被選中的機會。
收集數據:有多種方法可以收集數據,如面對面訪問、電話訪問、郵件調查或在線調查。
數據分析:一旦數據被收集,研究者會使用統計工具和技術進行分析,得出結論或洞見。
報告結果:分析完數據後,研究者會編寫報告或發布結果。報告通常會提供調查方法、樣本大小、誤差範圍和主要發現。
解釋誤差範圍:多數民調報告都會提供誤差範圍,例如“±3%”。這表示實際的結果有可能在報告結果的3%範圍內上下浮動。
民調調查的質量和可信度很大程度上取決於其設計和實施的方法。若是由專業和無偏見的組織進行,且使用科學的方法,那麼民調結果往往較為可靠。但即使是最高質量的民調也會有一定的誤差,因此解讀時應保持批判性思考。
為什麼要做民調?
民調提供了一種系統性的方式來了解大眾的意見、態度和信念。進行民調的原因多種多樣,以下是一些主要的動機:
政策制定和評估:政府和政策制定者進行民調,以了解公眾對某一議題或政策的看法。這有助於制定或調整政策,以反映大眾的需求和意見。
選舉和政治活動:政黨和候選人通常使用民調來評估自己在選舉中的地位,了解哪些議題對選民最重要,以及如何調整策略以吸引更多支持。
市場研究:企業和組織進行民調以了解消費者對產品、服務或品牌的態度,從而制定或調整市場策略。
社會科學研究:學者和研究者使用民調來了解人們的社會、文化和心理特征,以及其與行為的關係。
公眾與媒體的期望:民調提供了一種方式,使公眾、政府和企業得以了解社會的整體趨勢和態度。媒體也經常報導民調結果,提供公眾對當前議題的見解。
提供反饋和評估:無論是企業還是政府,都可以透過民調了解其表現、服務或政策的效果,並根據反饋進行改進。
預測和趨勢分析:民調可以幫助預測某些趨勢或行為的未來發展,如選舉結果、市場需求等。
教育和提高公眾意識:通過進行和公布民調,可以促使公眾對某一議題或問題有更深入的了解和討論。
民調可信嗎?
民意調查的結果數據隨處可見,尤其是政治性民調結果幾乎可說是天天在新聞上放送,對總統的滿意度下降了多少百分比,然而大家又信多少?
在景美市場的訪問中,我們了解到民眾對民調有一些普遍的觀點。大多數受訪者表示,他們對民調的可信度存有疑慮,主要原因是他們擔心政府可能會在調查中進行操控,以符合特定政治目標。
受訪者還提到,民意調查的結果通常不會對他們的投票意願產生影響。換句話說,他們的選擇通常受到更多因素的影響,例如候選人的政策立場和政府做事的認真與否,而不是單純依賴民調結果。
從訪問中我們可以得出的結論是,大多數民眾對民調持謹慎態度,並認為它們對他們的投票決策影響有限。
zestril 5mg price in india: lisinopril tablet – buy lisinopril 5 mg
lisinopril brand name in india: cost of lisinopril 2.5 mg – lisinopril 20 mg buy
http://cytotec.icu/# cytotec pills online
vibramycin 100 mg doxycycline 150 mg doxycycline generic
Nice post. I was checking constantly this blog and I am impressed! Extremely helpful info specifically the last part 🙂 I care for such information a lot. I was looking for this particular info for a very long time. Thank you and good luck.
http://canadapharm.life/# my canadian pharmacy canadapharm.life
canadian pharmacy king reviews: Canada Drugs Direct – best canadian pharmacy to order from canadapharm.life
buying prescription drugs in mexico online: mexican pharmacy – medication from mexico pharmacy mexicopharm.com
top online pharmacy india: India Post sending medicines to USA – best india pharmacy indiapharm.llc
buy medicines online in india indian pharmacy to usa top online pharmacy india indiapharm.llc
https://mexicopharm.com/# mexico pharmacy mexicopharm.com
canadianpharmacyworld: Canada pharmacy online – canadian online pharmacy reviews canadapharm.life
http://canadapharm.life/# canadian neighbor pharmacy canadapharm.life
canadian pharmacy: Pharmacies in Canada that ship to the US – cheap canadian pharmacy online canadapharm.life
Online medicine home delivery: indian pharmacy to usa – india pharmacy indiapharm.llc
mexican border pharmacies shipping to usa: Purple Pharmacy online ordering – mexican mail order pharmacies mexicopharm.com
https://mexicopharm.com/# mexican online pharmacies prescription drugs mexicopharm.com
canadian pharmacy ltd Cheapest drug prices Canada medication canadian pharmacy canadapharm.life
п»їbest mexican online pharmacies: Mexico pharmacy online – mexico drug stores pharmacies mexicopharm.com
https://mexicopharm.com/# mexican border pharmacies shipping to usa mexicopharm.com
buying prescription drugs in mexico: buying from online mexican pharmacy – mexico drug stores pharmacies mexicopharm.com
https://mexicopharm.com/# mexican pharmaceuticals online mexicopharm.com
I believe you have noted some very interesting details , regards for the post.
canadian pharmacy world: Canadian pharmacy best prices – canada drugstore pharmacy rx canadapharm.life
п»їlegitimate online pharmacies india: India Post sending medicines to USA – best india pharmacy indiapharm.llc
mexican pharmaceuticals online: Purple Pharmacy online ordering – п»їbest mexican online pharmacies mexicopharm.com
https://indiapharm.llc/# indian pharmacy indiapharm.llc
canadian pharmacy king: Canadian online pharmacy – canada pharmacy online canadapharm.life
https://indiapharm.llc/# world pharmacy india indiapharm.llc
buy prescription drugs from india india pharmacy mail order top online pharmacy india indiapharm.llc
Lovely just what I was searching for.Thanks to the author for taking his time on this one.
http://tadalafildelivery.pro/# tadalafil brand name in india
erection pills online: cheapest ed pills – medication for ed
sildenafil fast shipping: Buy generic 100mg Sildenafil online – 60 mg sildenafil
https://edpillsdelivery.pro/# cures for ed
sildenafil oral jelly 100mg kamagra kamagra oral jelly cheap kamagra
cheap kamagra: cheap kamagra – Kamagra 100mg
https://sildenafildelivery.pro/# sildenafil online mexico
Sight Care is a daily supplement proven in clinical trials and conclusive science to improve vision by nourishing the body from within. The SightCare formula claims to reverse issues in eyesight, and every ingredient is completely natural.
Vardenafil buy online: Levitra best price – Levitra 20 mg for sale
https://levitradelivery.pro/# Vardenafil buy online
Levitra online USA fast: Levitra best price – Cheap Levitra online
sildenafil tablets where to buy: Sildenafil price – sildenafil cream
https://tadalafildelivery.pro/# tadalafil 2.5 mg cost
I would like to thnkx for the efforts you have put in writing this blog. I am hoping the same high-grade blog post from you in the upcoming as well. In fact your creative writing abilities has inspired me to get my own blog now. Really the blogging is spreading its wings quickly. Your write up is a good example of it.
ed drugs list ed pills online erectile dysfunction medications
ed drugs compared: erection pills over the counter – best non prescription ed pills
http://tadalafildelivery.pro/# generic tadalafil 10mg
When I originally commented I clicked the -Notify me when new feedback are added- checkbox and now every time a comment is added I get 4 emails with the identical comment. Is there any method you can take away me from that service? Thanks!
best non prescription ed pills: ed pills online – ed meds online
https://kamagradelivery.pro/# Kamagra 100mg
sildenafil citrate generic viagra: Sildenafil price – sildenafil best price
http://kamagradelivery.pro/# cheap kamagra
There are certainly lots of particulars like that to take into consideration. That is a great level to carry up. I offer the thoughts above as basic inspiration but clearly there are questions like the one you bring up the place a very powerful thing will likely be working in trustworthy good faith. I don?t know if finest practices have emerged round things like that, but I’m sure that your job is clearly identified as a good game. Each girls and boys really feel the impression of just a second’s pleasure, for the remainder of their lives.
tadalafil 100mg online: Buy tadalafil online – cost of generic tadalafil
http://levitradelivery.pro/# Buy Vardenafil 20mg
Paxlovid over the counter Paxlovid buy online paxlovid pill
https://amoxil.guru/# amoxicillin generic
can i get clomid without prescription: Buy Clomid online – can you get clomid without a prescription
https://stromectol.guru/# ivermectin generic name
paxlovid pill paxlovid generic buy paxlovid online
https://stromectol.guru/# ivermectin india
https://stromectol.guru/# ivermectin topical
can i order cheap clomid tablets: clomid generic – can i order generic clomid without insurance
https://amoxil.guru/# amoxicillin 500 mg online
https://stromectol.guru/# ivermectin lotion for lice
Hello! I could have sworn I’ve been to this blog before but after browsing through some of the post I realized it’s new to me. Anyways, I’m definitely happy I found it and I’ll be book-marking and checking back frequently!
Wonderful website. A lot of useful info here. I’m sending it to several friends ans also sharing in delicious. And certainly, thanks for your effort!
http://amoxil.guru/# amoxicillin generic brand
buy paxlovid online buy paxlovid online paxlovid generic
Hello, you used to write great, but the last few posts have been kinda boring… I miss your super writings. Past several posts are just a little out of track! come on!
http://stromectol.guru/# stromectol how much it cost
ivermectin 4000: buy ivermectin online – ivermectin for sale
http://amoxil.guru/# amoxicillin from canada
http://prednisone.auction/# canine prednisone 5mg no prescription
http://paxlovid.guru/# Paxlovid over the counter
lasix medication Buy Lasix furosemide 100 mg
get generic propecia without dr prescription: Buy Finasteride 5mg – generic propecia pill
http://misoprostol.shop/# Misoprostol 200 mg buy online
https://furosemide.pro/# generic lasix
lisinopril medication otc: buy lisinopril canada – zestril 10mg
furosemide 100 mg: Buy Furosemide – furosemida 40 mg
https://azithromycin.store/# zithromax for sale cheap
lasix pills: Buy Lasix No Prescription – furosemide 40mg
ResumeHead is a resume writing company that helps you get ahead in your career. We are a group of certified resume writers who have extensive knowledge and experience in various fields and industries. We know how to highlight your strengths, achievements, and potential in a way that attracts the attention of hiring managers and recruiters. We also offer other services such as cover letter writing, LinkedIn profile optimization, and career coaching. Whether you need a resume for a new job, a promotion, or a career change, we can help you create a resume that showcases your unique value proposition. Contact us today and let us help you get the resume you deserve.
buy zithromax online cheap zithromax best price buy generic zithromax no prescription
http://azithromycin.store/# can you buy zithromax over the counter in canada
http://azithromycin.store/# where can i buy zithromax in canada
buy cytotec in usa: buy cytotec online – п»їcytotec pills online
order generic propecia pill: buy propecia – buy generic propecia no prescription
http://misoprostol.shop/# buy cytotec pills
I have been reading out many of your posts and i must say pretty good stuff. I will make sure to bookmark your site.
zithromax for sale us: zithromax tablets for sale – can you buy zithromax over the counter
home Buy finasteride 1mg cost generic propecia without dr prescription
https://azithromycin.store/# zithromax 500mg
buy propecia no prescription: Finasteride buy online – cost cheap propecia without insurance
What’s Happening i am new to this, I stumbled upon this I’ve found It positively useful and it has helped me out loads. I hope to contribute & help other users like its helped me. Great job.
where can i get zithromax: zithromax best price – zithromax antibiotic without prescription
http://finasteride.men/# propecia cheap
https://lisinopril.fun/# zestoretic 20 25
lisinopril 60 mg daily: High Blood Pressure – buy lisinopril online usa
buy lasix online Over The Counter Lasix lasix 100mg
http://misoprostol.shop/# buy cytotec over the counter
lisinopril prinivil zestril: zestril 20 mg – 1 lisinopril
https://finasteride.men/# buy propecia for sale
lisinopril 40 mg pill: zestoretic 20 mg – lisinopril generic
Hi, just required you to know I he added your site to my Google bookmarks due to your layout. But seriously, I believe your internet site has 1 in the freshest theme I??ve came across. It extremely helps make reading your blog significantly easier.
https://furosemide.pro/# lasix for sale
furosemide Buy Lasix No Prescription furosemide 40mg
lasix dosage: Buy Lasix – lasix side effects
https://lisinopril.fun/# lisinopril 20mg discount
http://furosemide.pro/# furosemide 40 mg
furosemide 40mg: Over The Counter Lasix – lasix 100mg
Thanks for another informative website. Where else could I get that kind of info written in such an ideal way? I’ve a project that I am just now working on, and I have been on the look out for such information.
http://finasteride.men/# get generic propecia without a prescription
where can i buy zithromax in canada: buy zithromax over the counter – can i buy zithromax online
generic propecia for sale buy cheap propecia pill buy cheap propecia prices
https://misoprostol.shop/# buy cytotec online
娛樂城
farmaci senza ricetta elenco: avanafil generico – acquistare farmaci senza ricetta
http://tadalafilitalia.pro/# top farmacia online
dove acquistare viagra in modo sicuro: viagra consegna in 24 ore pagamento alla consegna – viagra ordine telefonico
http://avanafilitalia.online/# п»їfarmacia online migliore
farmaci senza ricetta elenco avanafil farmacia online piГ№ conveniente
farmacie online autorizzate elenco: farmacia online – farmacia online piГ№ conveniente
http://avanafilitalia.online/# farmacia online più conveniente
comprare farmaci online all’estero: kamagra gel prezzo – п»їfarmacia online migliore
http://kamagraitalia.shop/# acquisto farmaci con ricetta
farmacia online: kamagra gel prezzo – acquisto farmaci con ricetta
But wanna comment that you have a very decent internet site, I like the style and design it actually stands out.
п»їfarmacia online migliore Farmacie a milano che vendono cialis senza ricetta farmacia online migliore
https://kamagraitalia.shop/# acquisto farmaci con ricetta
acquisto farmaci con ricetta: farmacia online spedizione gratuita – farmacie on line spedizione gratuita
http://farmaciaitalia.store/# farmacia online migliore
http://farmaciaitalia.store/# comprare farmaci online all’estero
farmacie online autorizzate elenco: Farmacie a milano che vendono cialis senza ricetta – farmacie online affidabili
farmaci senza ricetta elenco: kamagra oral jelly consegna 24 ore – farmacie on line spedizione gratuita
https://avanafilitalia.online/# farmacie online affidabili
You are my inspiration , I possess few web logs and infrequently run out from to post .
farmacia online migliore: Avanafil farmaco – farmacia online piГ№ conveniente
http://farmaciaitalia.store/# acquistare farmaci senza ricetta
It’s really a nice and useful piece of info. I’m glad that you shared this useful info with us. Please keep us informed like this. Thanks for sharing.
dove acquistare viagra in modo sicuro viagra prezzo pillole per erezione immediata
acquistare farmaci senza ricetta: kamagra oral jelly – migliori farmacie online 2023
https://kamagraitalia.shop/# farmacia online miglior prezzo
You have brought up a very great details, thankyou for the post.
gel per erezione in farmacia: alternativa al viagra senza ricetta in farmacia – cialis farmacia senza ricetta
https://sildenafilitalia.men/# viagra 50 mg prezzo in farmacia
http://farmaciaitalia.store/# farmacia online
indian pharmacy paypal pharmacy website india indian pharmacy
https://indiapharm.life/# mail order pharmacy india
buying prescription drugs in mexico online: п»їbest mexican online pharmacies – buying prescription drugs in mexico online
canadian pharmacy king reviews: canadian pharmacy ratings – best rated canadian pharmacy
https://canadapharm.shop/# canadian pharmacy world
http://canadapharm.shop/# certified canadian pharmacy
best india pharmacy: buy prescription drugs from india – top 10 pharmacies in india
http://mexicanpharm.store/# mexican pharmaceuticals online
mexican pharmacy: mexican drugstore online – medication from mexico pharmacy
legit canadian pharmacy online best canadian online pharmacy canadian pharmacies comparison
mexican online pharmacies prescription drugs: mexican pharmaceuticals online – pharmacies in mexico that ship to usa
canadian pharmacy no scripts: best canadian pharmacy – onlinecanadianpharmacy 24
I conceive this internet site has some very good info for everyone :D. “The public will believe anything, so long as it is not founded on truth.” by Edith Sitwell.
https://mexicanpharm.store/# mexican drugstore online
indian pharmacy paypal: buy medicines online in india – indianpharmacy com
indian pharmacy online: pharmacy website india – buy prescription drugs from india
http://canadapharm.shop/# prescription drugs canada buy online
https://canadapharm.shop/# canadian pharmacy 24
ed meds online canada: pharmacy rx world canada – legit canadian pharmacy
mexican border pharmacies shipping to usa: mexico drug stores pharmacies – mexican rx online
http://indiapharm.life/# top 10 pharmacies in india
canadianpharmacymeds com: canada drugs online review – canadian drug pharmacy
Great – I should certainly pronounce, impressed with your web site. I had no trouble navigating through all tabs and related info ended up being truly easy to do to access. I recently found what I hoped for before you know it at all. Reasonably unusual. Is likely to appreciate it for those who add forums or anything, site theme . a tones way for your customer to communicate. Excellent task..
https://indiapharm.life/# top online pharmacy india
india online pharmacy: indianpharmacy com – top online pharmacy india
northern pharmacy canada: legitimate canadian pharmacy online – canada drugs online
https://mexicanpharm.store/# mexico pharmacies prescription drugs
https://indiapharm.life/# world pharmacy india
pet meds without vet prescription canada: onlinecanadianpharmacy – best online canadian pharmacy
http://indiapharm.life/# world pharmacy india
2024娛樂城的創新趨勢
隨著2024年的到來,娛樂城業界正經歷著一場革命性的變遷。這一年,娛樂城不僅僅是賭博和娛樂的代名詞,更成為了科技創新和用戶體驗的集大成者。
首先,2024年的娛樂城極大地融合了最新的技術。增強現實(AR)和虛擬現實(VR)技術的引入,為玩家提供了沉浸式的賭博體驗。這種全新的遊戲方式不僅帶來視覺上的震撼,還為玩家創造了一種置身於真實賭場的感覺,而實際上他們可能只是坐在家中的沙發上。
其次,人工智能(AI)在娛樂城中的應用也達到了新高度。AI技術不僅用於增強遊戲的公平性和透明度,還在個性化玩家體驗方面發揮著重要作用。從個性化遊戲推薦到智能客服,AI的應用使得娛樂城更能滿足玩家的個別需求。
此外,線上娛樂城的安全性和隱私保護也獲得了顯著加強。隨著技術的進步,更加先進的加密技術和安全措施被用來保護玩家的資料和交易,從而確保一個安全可靠的遊戲環境。
2024年的娛樂城還強調負責任的賭博。許多平台採用了各種工具和資源來幫助玩家控制他們的賭博行為,如設置賭注限制、自我排除措施等,體現了對可持續賭博的承諾。
總之,2024年的娛樂城呈現出一個高度融合了技術、安全和負責任賭博的行業新面貌,為玩家提供了前所未有的娛樂體驗。隨著這些趨勢的持續發展,我們可以預見,娛樂城將不斷地創新和進步,為玩家帶來更多精彩和安全的娛樂選擇。
canadian online drugs: canadian pharmacy world reviews – reliable canadian online pharmacy
LeanBliss is a unique weight loss formula that promotes optimal weight and balanced blood sugar levels while curbing your appetite, detoxifying, and boosting your metabolism. https://leanblissbuynow.us/
pharmacy wholesalers canada canadian pharmacy canadian drug prices
mexico pharmacy: medicine in mexico pharmacies – mexico pharmacies prescription drugs
https://canadapharm.shop/# best canadian online pharmacy reviews
india pharmacy: indianpharmacy com – mail order pharmacy india
medicine in mexico pharmacies: mexican rx online – purple pharmacy mexico price list
cost of prednisone 40 mg: how much is prednisone 10 mg – prednisone 20 mg tablets coupon
https://prednisonepharm.store/# prednisone 50
buy cytotec over the counter: cytotec pills online – cytotec pills buy online
http://clomidpharm.shop/# order generic clomid prices
tamoxifen bone density raloxifene vs tamoxifen tamoxifen chemo
http://prednisonepharm.store/# buy prednisone no prescription
buy cytotec in usa: buy cytotec pills online cheap – buy cytotec online
F*ckin’ remarkable things here. I’m very glad to see your post. Thanks a lot and i am looking forward to contact you. Will you please drop me a mail?
http://prednisonepharm.store/# how to buy prednisone
http://nolvadex.pro/# tamoxifen alternatives premenopausal
who should take tamoxifen: tamoxifen cost – nolvadex pct
Mercedes for rent dubai
Dubai, a city known for its opulence and modernity, demands a mode of transportation that reflects its grandeur. For those seeking a cost-effective and reliable long-term solution, Somonion Rent Car LLC emerges as the premier choice for monthly car rentals in Dubai. With a diverse fleet ranging from compact cars to premium vehicles, the company promises an unmatched blend of affordability, flexibility, and personalized service.
Favorable Rental Conditions:
Understanding the potential financial strain of long-term car rentals, Somonion Rent Car LLC aims to make your journey more economical. The company offers flexible rental terms coupled with exclusive discounts for loyal customers. This commitment to affordability extends beyond the rental cost, as additional services such as insurance, maintenance, and repair ensure your safety and peace of mind throughout the duration of your rental.
A Plethora of Options:
Somonion Rent Car LLC boasts an extensive selection of vehicles to cater to diverse preferences and budgets. Whether you’re in the market for a sleek sedan or a spacious crossover, the company has the perfect car to complement your needs. The transparency in pricing, coupled with the ease of booking through their online platform, makes Somonion Rent Car LLC a hassle-free solution for those embarking on a long-term adventure in Dubai.
Car Rental Services Tailored for You:
Somonion Rent Car LLC doesn’t just offer cars; it provides a comprehensive range of rental services tailored to suit various occasions. From daily and weekly rentals to airport transfers and business travel, the company ensures that your stay in Dubai is not only comfortable but also exudes prestige. The fleet includes popular models such as the Nissan Altima 2018, KIA Forte 2018, Hyundai Elantra 2018, and the Toyota Camry Sport Edition 2020, all available for monthly rentals at competitive rates.
Featured Deals and Specials:
Somonion Rent Car LLC constantly updates its offerings to provide customers with the best deals. Featured cars like the Hyundai Sonata 2018 and Hyundai Santa Fe 2018 add a touch of luxury to your rental experience, with daily rates starting as low as AED 100. The company’s commitment to affordable luxury is further emphasized by the online booking system, allowing customers to secure the best deals in real-time through their website or by contacting the experts via phone or WhatsApp.
Conclusion:
Whether you’re a tourist looking to explore Dubai at your pace or a business traveler in need of a reliable and prestigious mode of transportation, Somonion Rent Car LLC stands as the go-to choice for monthly car rentals in Dubai. Unlock the ultimate mobility experience with Somonion, where affordability meets excellence, ensuring your journey through Dubai is as seamless and luxurious as the city itself. Contact Somonion Rent Car LLC today and embark on a journey where every mile is a testament to comfort, style, and unmatched service.
https://prednisonepharm.store/# prednisone 20 mg tablet
raloxifene vs tamoxifen tamoxifen alternatives buy nolvadex online
tamoxifen citrate pct: pct nolvadex – tamoxifen and depression
I visited a lot of website but I think this one has got something special in it in it
https://nolvadex.pro/# where to buy nolvadex
where can i buy zithromax in canada: buy zithromax online australia – zithromax prescription
http://nolvadex.pro/# how does tamoxifen work
http://cytotec.directory/# buy cytotec online fast delivery
where can i get prednisone over the counter: how can i get prednisone – prednisone pill 10 mg
http://zithromaxpharm.online/# zithromax price south africa
tamoxifen rash pictures should i take tamoxifen buy nolvadex online
tamoxifen dosage: tamoxifen menopause – tamoxifen skin changes
https://zithromaxpharm.online/# can you buy zithromax over the counter in australia
https://edpills.bid/# erection pills online
ed pills for sale: pills for ed – treatment of ed
online pharmacy mail order http://edpills.bid/# ed treatments
canadian online pharmacies ratings
http://edwithoutdoctorprescription.store/# non prescription ed pills
https://edpills.bid/# non prescription ed drugs
cheap erectile dysfunction pills: erectile dysfunction drug – buy ed pills online
medications with no prescription: prescription drug prices comparison – canadian mail order pharmacy
http://edpills.bid/# otc ed pills
erection pills: ed meds – best ed drug
overseas pharmacies that deliver to usa https://reputablepharmacies.online/# canadian prescription filled in the us
canada pharmacies online
http://reputablepharmacies.online/# nabp approved canadian pharmacies
BioPharma Blog provides news and analysis for biotech and biopharmaceutical executives. We cover topics like clinical trials, drug discovery and development, pharma marketing, FDA approvals and regulations, and more. https://biopharmablog.us/
pills for ed: cheap erectile dysfunction pills online – herbal ed treatment
https://edpills.bid/# erectile dysfunction drug
ed meds: cure ed – ed medications list
http://reputablepharmacies.online/# buy mexican drugs online
ed meds online without doctor prescription: ed meds online without doctor prescription – п»їprescription drugs
Watches World
Watches World: Elevating Luxury and Style with Exquisite Timepieces
Introduction:
Jewelry has always been a timeless expression of elegance, and nothing complements one’s style better than a luxurious timepiece. At Watches World, we bring you an exclusive collection of coveted luxury watches that not only tell time but also serve as a testament to your refined taste. Explore our curated selection featuring iconic brands like Rolex, Hublot, Omega, Cartier, and more, as we redefine the art of accessorizing.
A Dazzling Array of Luxury Watches:
Watches World offers an unparalleled range of exquisite timepieces from renowned brands, ensuring that you find the perfect accessory to elevate your style. Whether you’re drawn to the classic sophistication of Rolex, the avant-garde designs of Hublot, or the precision engineering of Patek Philippe, our collection caters to diverse preferences.
Customer Testimonials:
Our commitment to providing an exceptional customer experience is reflected in the reviews from our satisfied clientele. O.M. commends our excellent communication and flawless packaging, while Richard Houtman appreciates the helpfulness and courtesy of our team. These testimonials highlight our dedication to transparency, communication, and customer satisfaction.
New Arrivals:
Stay ahead of the curve with our latest additions, including the Tudor Black Bay Ceramic 41mm, Richard Mille RM35-01 Rafael Nadal NTPT Carbon Limited Edition, and the Rolex Oyster Perpetual Datejust 41mm series. These new arrivals showcase cutting-edge designs and impeccable craftsmanship, ensuring you stay on the forefront of luxury watch fashion.
Best Sellers:
Discover our best-selling watches, such as the Bulgari Serpenti Tubogas 35mm and the Cartier Panthere Medium Model. These timeless pieces combine elegance with precision, making them a staple in any sophisticated wardrobe.
Expert’s Selection:
Our experts have carefully curated a selection of watches, including the Cartier Panthere Small Model, Omega Speedmaster Moonwatch 44.25 mm, and Rolex Oyster Perpetual Cosmograph Daytona 40mm. These choices exemplify the epitome of watchmaking excellence and style.
Secured and Tracked Delivery:
At Watches World, we prioritize the safety of your purchase. Our secured and tracked delivery ensures that your exquisite timepiece reaches you in perfect condition, giving you peace of mind with every order.
Passionate Experts at Your Service:
Our team of passionate watch experts is dedicated to providing personalized service. From assisting you in choosing the perfect timepiece to addressing any inquiries, we are here to make your watch-buying experience seamless and enjoyable.
Global Presence:
With a presence in key cities around the world, including Dubai, Geneva, Hong Kong, London, Miami, Paris, Prague, Dublin, Singapore, and Sao Paulo, Watches World brings luxury timepieces to enthusiasts globally.
Conclusion:
Watches World goes beyond being an online platform for luxury watches; it is a destination where expertise, trust, and satisfaction converge. Explore our collection, and let our timeless timepieces become an integral part of your style narrative. Join us in redefining luxury, one exquisite watch at a time.
cheap erectile dysfunction pill: best pills for ed – buy erection pills
https://edwithoutdoctorprescription.store/# cialis without a doctor’s prescription
F*ckin¦ tremendous issues here. I¦m very satisfied to see your article. Thanks so much and i am taking a look forward to touch you. Will you please drop me a mail?
I see something truly interesting about your blog so I bookmarked.
pharmacy express online: canadian pharmaceuticals online safe – canadian pharmaceuticals online
Watches World: Elevating Luxury and Style with Exquisite Timepieces
Introduction:
Jewelry has always been a timeless expression of elegance, and nothing complements one’s style better than a luxurious timepiece. At Watches World, we bring you an exclusive collection of coveted luxury watches that not only tell time but also serve as a testament to your refined taste. Explore our curated selection featuring iconic brands like Rolex, Hublot, Omega, Cartier, and more, as we redefine the art of accessorizing.
A Dazzling Array of Luxury Watches:
Watches World offers an unparalleled range of exquisite timepieces from renowned brands, ensuring that you find the perfect accessory to elevate your style. Whether you’re drawn to the classic sophistication of Rolex, the avant-garde designs of Hublot, or the precision engineering of Patek Philippe, our collection caters to diverse preferences.
Customer Testimonials:
Our commitment to providing an exceptional customer experience is reflected in the reviews from our satisfied clientele. O.M. commends our excellent communication and flawless packaging, while Richard Houtman appreciates the helpfulness and courtesy of our team. These testimonials highlight our dedication to transparency, communication, and customer satisfaction.
New Arrivals:
Stay ahead of the curve with our latest additions, including the Tudor Black Bay Ceramic 41mm, Richard Mille RM35-01 Rafael Nadal NTPT Carbon Limited Edition, and the Rolex Oyster Perpetual Datejust 41mm series. These new arrivals showcase cutting-edge designs and impeccable craftsmanship, ensuring you stay on the forefront of luxury watch fashion.
Best Sellers:
Discover our best-selling watches, such as the Bulgari Serpenti Tubogas 35mm and the Cartier Panthere Medium Model. These timeless pieces combine elegance with precision, making them a staple in any sophisticated wardrobe.
Expert’s Selection:
Our experts have carefully curated a selection of watches, including the Cartier Panthere Small Model, Omega Speedmaster Moonwatch 44.25 mm, and Rolex Oyster Perpetual Cosmograph Daytona 40mm. These choices exemplify the epitome of watchmaking excellence and style.
Secured and Tracked Delivery:
At Watches World, we prioritize the safety of your purchase. Our secured and tracked delivery ensures that your exquisite timepiece reaches you in perfect condition, giving you peace of mind with every order.
Passionate Experts at Your Service:
Our team of passionate watch experts is dedicated to providing personalized service. From assisting you in choosing the perfect timepiece to addressing any inquiries, we are here to make your watch-buying experience seamless and enjoyable.
Global Presence:
With a presence in key cities around the world, including Dubai, Geneva, Hong Kong, London, Miami, Paris, Prague, Dublin, Singapore, and Sao Paulo, Watches World brings luxury timepieces to enthusiasts globally.
Conclusion:
Watches World goes beyond being an online platform for luxury watches; it is a destination where expertise, trust, and satisfaction converge. Explore our collection, and let our timeless timepieces become an integral part of your style narrative. Join us in redefining luxury, one exquisite watch at a time.
https://edpills.bid/# best medication for ed
non prescription erection pills: cheap erectile dysfunction – medication for ed
http://reputablepharmacies.online/# legitimate online pharmacy usa
http://canadianpharmacy.pro/# buy prescription drugs from canada cheap canadianpharmacy.pro
pharmacy website india: international medicine delivery from india – indianpharmacy com indianpharmacy.shop
News from the staff of the LA Reporter, including crime and investigative coverage of the South Bay and Harbor Area in Los Angeles County. https://lareporter.us/
http://indianpharmacy.shop/# world pharmacy india indianpharmacy.shop
reputable mexican pharmacies online: online mexican pharmacy – mexican pharmacy mexicanpharmacy.win
https://mexicanpharmacy.win/# mexico drug stores pharmacies mexicanpharmacy.win
canada medicine
Heya! I’m at work surfing around your blog from my new apple iphone! Just wanted to say I love reading through your blog and look forward to all your posts! Keep up the fantastic work!
https://indianpharmacy.shop/# Online medicine home delivery indianpharmacy.shop
http://canadianpharmacy.pro/# canadian pharmacy 24 canadianpharmacy.pro
indian pharmacy: india pharmacy – india pharmacy mail order indianpharmacy.shop
https://indianpharmacy.shop/# online pharmacy india indianpharmacy.shop
http://mexicanpharmacy.win/# mexico drug stores pharmacies mexicanpharmacy.win
http://canadianpharmacy.pro/# northern pharmacy canada canadianpharmacy.pro
compare prescription drug prices
https://indianpharmacy.shop/# best india pharmacy indianpharmacy.shop
indian pharmacies safe
https://indianpharmacy.shop/# cheapest online pharmacy india indianpharmacy.shop
Dead written written content, thank you for entropy. “The bravest thing you can do when you are not brave is to profess courage and act accordingly.” by Corra Harris.
https://mexicanpharmacy.win/# п»їbest mexican online pharmacies mexicanpharmacy.win
https://mexicanpharmacy.win/# medicine in mexico pharmacies mexicanpharmacy.win
buy prescription drugs from india
http://indianpharmacy.shop/# Online medicine home delivery indianpharmacy.shop
http://mexicanpharmacy.win/# mexican pharmacy mexicanpharmacy.win
buy medicines online in india
top 10 online pharmacy in india Order medicine from India to USA п»їlegitimate online pharmacies india indianpharmacy.shop
http://canadianpharmacy.pro/# canadianpharmacyworld canadianpharmacy.pro
Yolonews.us covers local news in Yolo County, California. Keep up with all business, local sports, outdoors, local columnists and more. https://yolonews.us/
I got what you mean , appreciate it for posting.Woh I am lucky to find this website through google.
http://mexicanpharmacy.win/# mexican mail order pharmacies mexicanpharmacy.win
indian pharmacy online
2024全新上線❰戰神賽特老虎機❱ – ATG賽特玩法說明介紹
❰戰神賽特老虎機❱是由ATG電子獨家開發的古埃及風格線上老虎機,在傳說中戰神賽特是「力量之神」與奈芙蒂斯女神結成連理,共同守護古埃及的奇幻秘寶,只有被選中的冒險者才能進入探險。
❰戰神賽特老虎機❱ – ATG賽特介紹
2024最新老虎機【戰神塞特】- ATG電子 X 富遊娛樂城
❰戰神賽特老虎機❱ – ATG電子
線上老虎機系統 : ATG電子
發行年分 : 2024年1月
最大倍數 : 51000倍
返還率 : 95.89%
支付方式 : 全盤倍數、消除掉落
最低投注金額 : 0.4元
最高投注金額 : 2000元
可否選台 : 是
可選台台數 : 350台
免費遊戲 : 選轉觸發+購買特色
❰戰神賽特老虎機❱ 賠率說明
戰神塞特老虎機賠率算法非常簡單,玩家們只需要不斷的轉動老虎機,成功消除物件即可贏分,得分賠率依賠率表計算。
當盤面上沒有物件可以消除時,倍數符號將會相加形成總倍數!該次旋轉的總贏分即為 : 贏分 X 總倍數。
積分方式如下 :
贏分=(單次押注額/20) X 物件賠率
EX : 單次押注額為1,盤面獲得12個戰神賽特倍數符號法老魔眼
贏分= (1/20) X 1000=50
以下為各個得分符號數量之獎金賠率 :
得分符號 獎金倍數 得分符號 獎金倍數
戰神賽特倍數符號聖甲蟲 6 2000
5 100
4 60 戰神賽特倍數符號黃寶石 12+ 200
10-11 30
8-9 20
戰神賽特倍數符號荷魯斯之眼 12+ 1000
10-11 500
8-9 200 戰神賽特倍數符號紅寶石 12+ 160
10-11 24
8-9 16
戰神賽特倍數符號眼鏡蛇 12+ 500
10-11 200
8-9 50 戰神賽特倍數符號紫鑽石 12+ 100
10-11 20
8-9 10
戰神賽特倍數符號神箭 12+ 300
10-11 100
8-9 40 戰神賽特倍數符號藍寶石 12+ 80
10-11 18
8-9 8
戰神賽特倍數符號屠鐮刀 12+ 240
10-11 40
8-9 30 戰神賽特倍數符號綠寶石 12+ 40
10-11 15
8-9 5
❰戰神賽特老虎機❱ 賠率說明(橘色數值為獲得數量、黑色數值為得分賠率)
ATG賽特 – 特色說明
ATG賽特 – 倍數符號獎金加乘
玩家們在看到盤面上出現倍數符號時,務必把握機會加速轉動ATG賽特老虎機,倍數符號會隨機出現2到500倍的隨機倍數。
當盤面無法在消除時,這些倍數總和會相加,乘上當時累積之獎金,即為最後得分總額。
倍數符號會出現在主遊戲和免費遊戲當中,玩家們千萬別錯過這個可以瞬間將得獎金額拉高的好機會!
ATG賽特 – 倍數符號獎金加乘
ATG賽特 – 倍數符號圖示
ATG賽特 – 進入神秘金字塔開啟免費遊戲
戰神賽特倍數符號聖甲蟲
❰戰神賽特老虎機❱ 免費遊戲符號
在古埃及神話中,聖甲蟲又稱為「死亡之蟲」,它被當成了天球及重生的象徵,守護古埃及的奇幻秘寶。
當玩家在盤面上,看見越來越多的聖甲蟲時,千萬不要膽怯,只需在牌面上斬殺4~6個ATG賽特免費遊戲符號,就可以進入15場免費遊戲!
在免費遊戲中若轉出3~6個聖甲蟲免費遊戲符號,可額外獲得5次免費遊戲,最高可達100次。
當玩家的累積贏分且盤面有倍數物件時,盤面上的所有倍數將會加入總倍數!
ATG賽特 – 選台模式贏在起跑線
為避免神聖的寶物被盜墓者奪走,富有智慧的法老王將金子塔內佈滿迷宮,有的設滿機關讓盜墓者寸步難行,有的暗藏機關可以直接前往存放神秘寶物的暗房。
ATG賽特老虎機設有350個機檯供玩家選擇,這是連魔龍老虎機、忍老虎機都給不出的機台數量,為的就是讓玩家,可以隨時進入神秘的古埃及的寶藏聖域,挖掘長眠已久的神祕寶藏。
【戰神塞特老虎機】選台模式
❰戰神賽特老虎機❱ 選台模式
ATG賽特 – 購買免費遊戲挖掘秘寶
玩家們可以使用當前投注額的100倍購買免費遊戲!進入免費遊戲再也不是虛幻。獎勵與一般遊戲相同,且購買後遊戲將自動開始,直到場次和獎金發放完畢為止。
有購買免費遊戲需求的玩家們,立即點擊「開始」,啟動神秘金字塔裡的古埃及祕寶吧!
【戰神塞特老虎機】購買特色
❰戰神賽特老虎機❱ 購買特色
戰神賽特試玩推薦
看完了❰戰神賽特老虎機❱介紹之後,玩家們是否也蓄勢待發要進入古埃及的世界,一探神奇秘寶探險之旅。
本次ATG賽特與線上娛樂城推薦第一名的富遊娛樂城合作,只需要加入會員,即可領取到168體驗金,免費試玩420轉!
https://canadianpharmacy.pro/# reliable canadian pharmacy canadianpharmacy.pro
https://canadianpharmacy.pro/# canada drugs online review canadianpharmacy.pro
best canadian drug prices
http://canadianpharmacy.pro/# canadian pharmacy india canadianpharmacy.pro
mail order pharmacy india
https://mexicanpharmacy.win/# pharmacies in mexico that ship to usa mexicanpharmacy.win
https://mexicanpharmacy.win/# buying from online mexican pharmacy mexicanpharmacy.win
reputable indian pharmacies
https://indianpharmacy.shop/# top online pharmacy india indianpharmacy.shop
http://canadianpharmacy.pro/# pharmacies in canada that ship to the us canadianpharmacy.pro
http://mexicanpharmacy.win/# medication from mexico pharmacy mexicanpharmacy.win
buy medicines online in india
Acheter mГ©dicaments sans ordonnance sur internet: pharmacie ouverte 24/24 – Pharmacie en ligne livraison gratuite
Viagra sans ordonnance pharmacie France: viagra sans ordonnance – Le gГ©nГ©rique de Viagra
https://cialissansordonnance.shop/# Pharmacie en ligne fiable
pharmacie ouverte 24/24: kamagra livraison 24h – acheter mГ©dicaments Г l’Г©tranger
https://viagrasansordonnance.pro/# Quand une femme prend du Viagra homme
Pharmacies en ligne certifiГ©es
acheter medicament a l etranger sans ordonnance: cialis sans ordonnance – pharmacie ouverte
Pharmacie en ligne pas cher levitra generique prix en pharmacie Pharmacie en ligne fiable
https://viagrasansordonnance.pro/# Viagra vente libre allemagne
Viagra vente libre pays: Meilleur Viagra sans ordonnance 24h – Viagra 100mg prix
pharmacie ouverte kamagra livraison 24h п»їpharmacie en ligne
https://acheterkamagra.pro/# pharmacie ouverte 24/24
п»їpharmacie en ligne: kamagra 100mg prix – Pharmacies en ligne certifiГ©es
http://pharmadoc.pro/# Pharmacie en ligne France
Pharmacie en ligne France
https://viagrasansordonnance.pro/# Quand une femme prend du Viagra homme
Viagra sans ordonnance 24h Amazon: Meilleur Viagra sans ordonnance 24h – Viagra vente libre pays
Pharmacie en ligne pas cher: levitra generique prix en pharmacie – Pharmacie en ligne livraison 24h
https://viagrasansordonnance.pro/# Viagra vente libre allemagne
п»їpharmacie en ligne: Pharmacies en ligne certifiees – acheter medicament a l etranger sans ordonnance
http://acheterkamagra.pro/# Pharmacie en ligne pas cher
20 mg of prednisone: prednisone 54899 – prednisone 10mg canada
http://azithromycin.bid/# zithromax generic cost
amoxicillin no prescription: amoxicillin generic – amoxicillin without a doctors prescription
https://ivermectin.store/# stromectol ebay
http://azithromycin.bid/# generic zithromax medicine
cost cheap clomid no prescription: can you buy generic clomid pill – buy clomid without prescription
zithromax 1000 mg online: zithromax capsules 250mg – where can you buy zithromax
Дома АВС – Ваш уютный уголок
Мы строим не просто дома, мы создаем пространство, где каждый уголок будет наполнен комфортом и радостью жизни. Наш приоритет – не просто предоставить место для проживания, а создать настоящий дом, где вы будете чувствовать себя счастливыми и уютно.
В нашем информационном разделе “ПРОЕКТЫ” вы всегда найдете вдохновение и новые идеи для строительства вашего будущего дома. Мы постоянно работаем над тем, чтобы предложить вам самые инновационные и стильные проекты.
Мы убеждены, что основа хорошего дома – это его дизайн. Поэтому мы предоставляем услуги опытных дизайнеров-архитекторов, которые помогут вам воплотить все ваши идеи в жизнь. Наши архитекторы и персональные консультанты всегда готовы поделиться своим опытом и предложить функциональные и комфортные решения для вашего будущего дома.
Мы стремимся сделать весь процесс строительства максимально комфортным для вас. Наша команда предоставляет детализированные сметы, разрабатывает четкие этапы строительства и осуществляет контроль качества на каждом этапе.
Для тех, кто ценит экологичность и близость к природе, мы предлагаем деревянные дома премиум-класса. Используя клееный брус и оцилиндрованное бревно, мы создаем уникальные и здоровые условия для вашего проживания.
Тем, кто предпочитает надежность и многообразие форм, мы предлагаем дома из камня, блоков и кирпичной кладки.
Для практичных и ценящих свое время людей у нас есть быстровозводимые каркасные дома и эконом-класса. Эти решения обеспечат вас комфортным проживанием в кратчайшие сроки.
С Домами АВС создайте свой уютный уголок, где каждый момент жизни будет наполнен радостью и удовлетворением
https://clomiphene.icu/# where to buy generic clomid prices
zithromax over the counter uk: zithromax z-pak price without insurance – buy zithromax no prescription
http://azithromycin.bid/# zithromax buy online no prescription
amoxicillin azithromycin: how much is amoxicillin – can you buy amoxicillin over the counter in canada
amoxicillin 500 mg purchase without prescription: buy amoxicillin 500mg – can you buy amoxicillin over the counter
https://clomiphene.icu/# where buy generic clomid
prednisone coupon: prednisone 100 mg – online order prednisone
I really lucky to find this site on bing, just what I was looking for : D also saved to favorites.
https://amoxicillin.bid/# amoxicillin for sale online
amoxicillin 500 mg brand name: prescription for amoxicillin – amoxil generic
digiyumi.com
Fang Jifan은 전초 기지로 Tianjin Wei에 도착했고 즉시 이곳에서 거룩한 운전자를 기다렸습니다.
cost generic clomid without a prescription buy generic clomid pill how to get generic clomid without a prescription
zithromax prescription in canada: zithromax 250 mg pill – purchase zithromax online
http://clomiphene.icu/# order generic clomid pills
where can i get generic clomid without a prescription: how can i get cheap clomid – how to get generic clomid
rivipaolo.com
Hongzhi 황제는 Li Dongyang도 Xie Qian도 Liu Jie를 신뢰하지 않는 것을 보았습니다.
zithromax 500 zithromax 250mg zithromax generic cost
how to get generic clomid no prescription: how to get cheap clomid without rx – can i buy clomid without prescription
http://ivermectin.store/# generic ivermectin cream
https://clomiphene.icu/# can i get clomid without dr prescription
canadian pharmacy no scripts: Canada Pharmacy online – trustworthy canadian pharmacy canadianpharm.store
http://mexicanpharm.shop/# reputable mexican pharmacies online mexicanpharm.shop
mexico drug stores pharmacies: medicine in mexico pharmacies – п»їbest mexican online pharmacies mexicanpharm.shop
Some genuinely fantastic information, Gladiolus I found this. “Life is divided into the horrible and the miserable.” by Woody Allen.
I like this post, enjoyed this one appreciate it for posting.
medicine in mexico pharmacies: Online Pharmacies in Mexico – mexico drug stores pharmacies mexicanpharm.shop
https://mexicanpharm.shop/# mexican border pharmacies shipping to usa mexicanpharm.shop
cheap canadian pharmacy: Canadian International Pharmacy – ed drugs online from canada canadianpharm.store
www canadianonlinepharmacy: Certified Online Pharmacy Canada – canadian discount pharmacy canadianpharm.store
https://mexicanpharm.shop/# mexico pharmacies prescription drugs mexicanpharm.shop
https://mexicanpharm.shop/# medication from mexico pharmacy mexicanpharm.shop
buying drugs from canada: canada online pharmacy – legal canadian pharmacy online canadianpharm.store
Very interesting information!Perfect just what I was looking for!
https://indianpharm.store/# indian pharmacies safe indianpharm.store
medicine in mexico pharmacies mexico drug stores pharmacies mexican online pharmacies prescription drugs mexicanpharm.shop
online pharmacy canada: Best Canadian online pharmacy – onlinepharmaciescanada com canadianpharm.store
п»їlegitimate online pharmacies india: international medicine delivery from india – п»їlegitimate online pharmacies india indianpharm.store
tsrrub.com
그러나 그는 견딜 수 없었고, 그의 아들은 다른 사람들의 손에 총이 되었습니다.
http://mexicanpharm.shop/# buying from online mexican pharmacy mexicanpharm.shop
canadian pharmacy ltd: Pharmacies in Canada that ship to the US – is canadian pharmacy legit canadianpharm.store
lso thank you for allowing me to comment!.<a href="https://www.toolbarqueries.google.dm/url?sa=t
indian pharmacy online: international medicine delivery from india – buy medicines online in india indianpharm.store
mexican rx online: Online Pharmacies in Mexico – mexico drug stores pharmacies mexicanpharm.shop
http://mexicanpharm.shop/# mexican pharmaceuticals online mexicanpharm.shop
buying prescription drugs in mexico Certified Pharmacy from Mexico mexico drug stores pharmacies mexicanpharm.shop
best canadian pharmacy online: Certified Online Pharmacy Canada – canadian pharmacies online canadianpharm.store
http://indianpharm.store/# top online pharmacy india indianpharm.store
northern pharmacy canada: Canada Pharmacy online – canadian pharmacy tampa canadianpharm.store
I like what you guys tend to be up too. This type of clever work and exposure! Keep up the fantastic works guys I’ve you guys to blogroll.
online shopping pharmacy india: pharmacy website india – top online pharmacy india indianpharm.store
https://indianpharm.store/# buy medicines online in india indianpharm.store
Hello! Do you know if they make any plugins to help with SEO? I’m trying to get my blog to rank for some targeted keywords but I’m not seeing very good gains. If you know of any please share. Kudos!
mexican online pharmacies prescription drugs: Online Mexican pharmacy – pharmacies in mexico that ship to usa mexicanpharm.shop
mexican drugstore online: mexico pharmacies prescription drugs – mexican online pharmacies prescription drugs mexicanpharm.shop
https://mexicanpharm.shop/# buying prescription drugs in mexico mexicanpharm.shop
legitimate canadian pharmacy online: northern pharmacy canada – canadian discount pharmacy canadianpharm.store
https://mexicanpharm.shop/# best mexican online pharmacies mexicanpharm.shop
world pharmacy india: Indian pharmacy to USA – indian pharmacy online indianpharm.store
top 10 pharmacies in india: top 10 pharmacies in india – п»їlegitimate online pharmacies india indianpharm.store
pharmacy website india: india online pharmacy – indian pharmacy indianpharm.store
kinoboomhd.com
종합시험에서 3등을 했지만 탕인은 조금도 달갑지 않았다.
http://canadianpharm.store/# canadapharmacyonline canadianpharm.store
northern pharmacy canada: Canadian Pharmacy – canadian pharmacy canadianpharm.store
Merely a smiling visitant here to share the love (:, btw outstanding layout.
https://indianpharm.store/# indian pharmacy indianpharm.store
https://mexicanpharm.shop/# mexican rx online mexicanpharm.shop
I’ve recently started a blog, the information you offer on this site has helped me tremendously. Thank you for all of your time & work.
indian pharmacies safe: international medicine delivery from india – reputable indian online pharmacy indianpharm.store
We stumbled over here different website and thought I might check things out. I like what I see so now i am following you. Look forward to finding out about your web page for a second time.
pharmacy in canada: canadian trust pharmacy – best canadian drug prices
canadian drug store prices: canadian drug store coupon – canada drugs online reviews
online pharmacy without a prescription: canadiandrugstore.com – most popular canadian pharmacy
canadian pharcharmy online: prescription pricing – online pharmacy without a prescription
https://canadadrugs.pro/# recommended canadian pharmacies
certainly like your web-site but you have to test the spelling on several of your posts. A number of them are rife with spelling issues and I in finding it very troublesome to tell the truth however I’ll certainly come back again.
homefronttoheartland.com
그러나 류 씨는 운이 좋지 않은 유일한 아들이었습니다.
legal online pharmacies: northwest canadian pharmacy – best canadian online pharmacy
http://canadadrugs.pro/# international pharmacies that ship to the usa
thecanadianpharmacy com: no 1 canadian pharcharmy online – mexican online pharmacy
Thanks for helping out, good information. “Our individual lives cannot, generally, be works of art unless the social order is also.” by Charles Horton Cooley.
http://canadadrugs.pro/# most reputable canadian pharmacy
safe canadian online pharmacy: canadian pharmacies for viagra – drug stores canada
best online pharmacy stores good online mexican pharmacy discount drugs online pharmacy
canada drugs online reviews: online discount pharmacy – discount mail order pharmacy
https://canadadrugs.pro/# accutane mexican pharmacy
online drugstore coupon: pharmacy cost comparison – canadian pharmacy direct
http://canadadrugs.pro/# discount online pharmacy
mail order prescription drugs from canada: pharmacies withour prescriptions – discount online pharmacy
Your style is so unique compared to many other people. Thank you for publishing when you have the opportunity,Guess I will just make this bookmarked.2
娛樂城
overseas pharmacy: list of canadian pharmacies online – prescriptions from canada without
https://canadadrugs.pro/# canadian pharmacy tadalafil
canadian discount drugs: best canadian pharcharmy online – prescription drug prices comparison
https://canadadrugs.pro/# north canadian pharmacy
world pharmacy: canadian pharmacy online canada – online medications
no prescription drugs canada: cheap prescriptions – list of approved canadian pharmacies
https://canadadrugs.pro/# overseas pharmacy
online pharmacies no prescriptions: canadian meds without prescription – best canadian pharmacy no prescription
What makes Sumatra Slim Belly Tonic even more unique is its inspiration from the beautiful Indonesian island of Sumatra. This supplement incorporates ingredients that are indigenous to this stunning island, including the exotic blue spirulina. How amazing is that? By harnessing the power of these rare and natural ingredients, Sumatra Slim Belly Tonic provides you with a weight loss solution that is both effective and enchanting.
http://canadadrugs.pro/# global pharmacy canada
https://canadadrugs.pro/# buy prescription drugs canada
best mail order pharmacies: best online pharmacies reviews – high street discount pharmacy
reputable indian online pharmacy: indian pharmacy paypal – top 10 pharmacies in india
https://edwithoutdoctorprescription.pro/# ed prescription drugs
homefronttoheartland.com
Wang Bushi는 웃으며 “세단 의자를 준비하십시오. 나 Wang Bushi는 Fang Jifan과 싸울 것입니다!”
legal to buy prescription drugs without prescription: cheap cialis – cialis without a doctor’s prescription
digiapk.com
Zhu Houzhao는 머리를 긁적이며 쓰라린 미소를 지을 수 없었습니다. “그럼 내가 졌으니 …”
https://certifiedpharmacymexico.pro/# buying from online mexican pharmacy
п»їbest mexican online pharmacies: mexican mail order pharmacies – medication from mexico pharmacy
http://edwithoutdoctorprescription.pro/# generic viagra without a doctor prescription
canadian neighbor pharmacy: my canadian pharmacy review – canadian king pharmacy
http://canadianinternationalpharmacy.pro/# canadian pharmacy no scripts
best ways to make money online
Understanding the processes and protocols within a Professional Tenure Committee (PTC) is crucial for faculty members. This Frequently Asked Questions (FAQ) guide aims to address common queries related to PTC procedures, voting, and membership.
1. Why should members of the PTC fill out vote justification forms explaining their votes?
Vote justification forms provide transparency in decision-making. Members articulate their reasoning, fostering a culture of openness and ensuring that decisions are well-founded and understood by the academic community.
2. How can absentee ballots be cast?
To accommodate absentee voting, PTCs may implement secure electronic methods or designated proxy voters. This ensures that faculty members who cannot physically attend meetings can still contribute to decision-making processes.
3. How will additional members of PTCs be elected in departments with fewer than four tenured faculty members?
In smaller departments, creative solutions like rotating roles or involving faculty from related disciplines can be explored. Flexibility in election procedures ensures representation even in departments with fewer tenured faculty members.
4. Can a faculty member on OCSA or FML serve on a PTC?
Faculty members involved in other committees like the Organization of Committee on Student Affairs (OCSA) or Family and Medical Leave (FML) can serve on a PTC, but potential conflicts of interest should be carefully considered and managed.
5. Can an abstention vote be cast at a PTC meeting?
Yes, PTC members have the option to abstain from voting if they feel unable to take a stance on a particular matter. This allows for ethical decision-making and prevents uninformed voting.
6. What constitutes a positive or negative vote in PTCs?
A positive vote typically indicates approval or agreement, while a negative vote signifies disapproval or disagreement. Clear definitions and guidelines within each PTC help members interpret and cast their votes accurately.
7. What constitutes a quorum in a PTC?
A quorum, the minimum number of members required for a valid meeting, is essential for decision-making. Specific rules about quorum size are usually outlined in the PTC’s governing documents.
Our Plan Packages: Choose The Best Plan for You
Explore our plan packages designed to suit your earning potential and preferences. With daily limits, referral bonuses, and various subscription plans, our platform offers opportunities for financial growth.
Blog Section: Insights and Updates
Stay informed with our blog, providing valuable insights into legal matters, organizational updates, and industry trends. Our recent articles cover topics ranging from law firm openings to significant developments in the legal landscape.
Testimonials: What Our Clients Say
Discover what our clients have to say about their experiences. Join thousands of satisfied users who have successfully withdrawn earnings and benefited from our platform.
Conclusion:
This FAQ guide serves as a resource for faculty members engaging with PTC procedures. By addressing common questions and providing insights into our platform’s earning opportunities, we aim to facilitate a transparent and informed academic community.
https://edpill.cheap/# drugs for ed
I don’t even know how I ended up here, but I thought this post was good. I don’t know who you are but certainly you’re going to a famous blogger if you aren’t already 😉 Cheers!
https://edpill.cheap/# cheap erectile dysfunction
п»їbest mexican online pharmacies: purple pharmacy mexico price list – mexican border pharmacies shipping to usa
escrow pharmacy canada: canada drugstore pharmacy rx – canadian pharmacy meds reviews
https://certifiedpharmacymexico.pro/# mexican rx online
Good – I should certainly pronounce, impressed with your site. I had no trouble navigating through all tabs as well as related information ended up being truly easy to do to access. I recently found what I hoped for before you know it in the least. Quite unusual. Is likely to appreciate it for those who add forums or anything, website theme . a tones way for your customer to communicate. Excellent task.
This is my first time pay a quick visit at here and i am really happy to read everthing at one place .-vox live 2ix25
http://canadianinternationalpharmacy.pro/# canadadrugpharmacy com
india online pharmacy: indian pharmacies safe – top online pharmacy india
Hey there, You’ve done a great job. I’ll certainly digg it and personally suggest to my friends. I’m confident they will be benefited from this web site.
https://canadianinternationalpharmacy.pro/# canadian pharmacy store
ed treatment review: best otc ed pills – ed medications online
http://edpill.cheap/# buying ed pills online
wonderful post.Ne’er knew this, appreciate it for letting me know.
hello there and thank you for your information – I’ve definitely picked up anything new from right here. I did however expertise a few technical points using this web site, as I experienced to reload the website lots of times previous to I could get it to load correctly. I had been wondering if your web host is OK? Not that I’m complaining, but slow loading instances times will often affect your placement in google and can damage your quality score if advertising and marketing with Adwords. Anyway I’m adding this RSS to my email and could look out for a lot more of your respective interesting content. Ensure that you update this again soon..
https://certifiedpharmacymexico.pro/# buying prescription drugs in mexico
https://edpill.cheap/# best pills for ed
buy prescription drugs without doctor: prescription drugs without doctor approval – prescription drugs online
http://certifiedpharmacymexico.pro/# buying prescription drugs in mexico
http://edpill.cheap/# how to cure ed
Hello There. I found your blog using msn. This is an extremely well written article. I will make sure to bookmark it and come back to read more of your useful info. Thanks for the post. I will definitely comeback.
https://certifiedpharmacymexico.pro/# mexican mail order pharmacies
http://edwithoutdoctorprescription.pro/# prescription drugs online without
best canadian pharmacy online: canadian pharmacy drugs online – canadian pharmacies that deliver to the us
mexican rx online mexican pharmacy mexico drug stores pharmacies
this-is-a-small-world.com
갑자기 긴장이 풀리는 것 같았고, 긴장했던 신경도 풀렸다.
https://medicinefromindia.store/# pharmacy website india
canadian 24 hour pharmacy canada pharmacy online canadian pharmacy in canada
https://edwithoutdoctorprescription.pro/# prescription drugs online without
http://medicinefromindia.store/# п»їlegitimate online pharmacies india
canadian pharmacy antibiotics canadian pharmacy com recommended canadian pharmacies
https://canadianinternationalpharmacy.pro/# canadian pharmacy uk delivery
canadian pharmacy meds review: canadian pharmacy meds reviews – canadian pharmacy scam
I wanted to thank you for this great read!! I definitely enjoying every little bit of it I have you bookmarked to check out new stuff you post…
https://canadianinternationalpharmacy.pro/# online canadian pharmacy review
http://canadianinternationalpharmacy.pro/# canadian pharmacies comparison
Wow! Thank you! I continually wanted to write on my website something like that. Can I implement a portion of your post to my site?
http://edpill.cheap/# best erectile dysfunction pills
mexican drugstore online medicine in mexico pharmacies medicine in mexico pharmacies
mexican online pharmacies prescription drugs medicine in mexico pharmacies buying prescription drugs in mexico
http://mexicanph.shop/# mexican rx online
reputable mexican pharmacies online
mexico pharmacy buying prescription drugs in mexico mexican mail order pharmacies
restaurant-lenvol.net
리이는 그대로 땅바닥에 쓰러졌지만 아무 말 없이 다시 똑바로 무릎을 꿇었다.
mexican mail order pharmacies mexican rx online mexican drugstore online
purple pharmacy mexico price list mexican pharmacy mexico drug stores pharmacies
rivipaolo.com
밖에는 급한 발걸음이 있었고 Zhu Houzhao는 “비켜”라고 말했습니다.
mexican pharmacy mexican rx online buying from online mexican pharmacy
http://mexicanph.com/# mexico drug stores pharmacies
mexico drug stores pharmacies
mexican border pharmacies shipping to usa mexican rx online mexico pharmacies prescription drugs
п»їbest mexican online pharmacies mexico drug stores pharmacies buying prescription drugs in mexico online
mexico pharmacies prescription drugs mexico drug stores pharmacies mexican pharmaceuticals online
http://mexicanph.com/# buying prescription drugs in mexico
mexican pharmaceuticals online
Wow! This can be one particular of the most beneficial blogs We have ever arrive across on this subject. Actually Excellent. I’m also an expert in this topic therefore I can understand your effort.
Watches World
Watches Planet
Customer Reviews Shine light on WatchesWorld Adventure
At Our Watch Boutique, client fulfillment isn’t just a target; it’s a shining evidence to our devotion to perfection. Let’s dive into what our cherished patrons have to communicate about their journeys, illuminating on the flawless service and amazing watches we provide.
O.M.’s Review Testimonial: A Seamless Adventure
“Very good communication and follow along throughout the procedure. The watch was impeccably packed and in perfect. I would certainly work with this teamwork again for a timepiece purchase.
O.M.’s declaration illustrates our dedication to comms and careful care in delivering clocks in pristine condition. The reliance built with O.M. is a cornerstone of our patron relations.
Richard Houtman’s Informative Review: A Individual Contact
“I dealt with Benny, who was exceedingly beneficial and civil at all times, keeping me regularly notified of the procession. Advancing, even though I ended up sourcing the timepiece locally, I would still surely recommend Benny and the company progressing.
Richard Houtman’s interaction spotlights our tailored approach. Benny’s support and continuous comms exhibit our devotion to ensuring every patron feels appreciated and apprised.
Customer’s Streamlined Assistance Testimonial: A Seamless Transaction
“A very efficient and productive service. Kept me informed on the purchase development.
Our commitment to efficiency is echoed in this client’s commentary. Keeping patrons apprised and the effortless progress of acquisitions are integral to the Our Watch Boutique experience.
Explore Our Current Selections
Audemars Piguet Royal Oak Selfwinding 37mm
A gorgeous piece at €45,900, this 2022 edition (REF: 15551ST.ZZ.1356ST.05) invites you to add it to your shopping cart and elevate your set.
Hublot Classic Fusion Green Titanium Chronograph 45mm
Priced at €8,590 in 2024 (REF: 521.NX.8970.RX), this Hublot creation is a mixture of styling and innovation, awaiting your application.
mexican rx online mexican online pharmacies prescription drugs mexico drug stores pharmacies
buying from online mexican pharmacy mexican rx online mexico drug stores pharmacies
ST666
best online pharmacies in mexico mexican pharmaceuticals online mexican online pharmacies prescription drugs
medication from mexico pharmacy mexico drug stores pharmacies pharmacies in mexico that ship to usa
purple pharmacy mexico price list reputable mexican pharmacies online mexico pharmacy
mexico pharmacy pharmacies in mexico that ship to usa mexico drug stores pharmacies
mexico pharmacies prescription drugs mexico drug stores pharmacies buying from online mexican pharmacy
best mexican online pharmacies mexico drug stores pharmacies mexican drugstore online
http://mexicanph.com/# mexico drug stores pharmacies
pharmacies in mexico that ship to usa
mexico pharmacy best online pharmacies in mexico medication from mexico pharmacy
mexico drug stores pharmacies mexico drug stores pharmacies mexico pharmacy
mexican pharmaceuticals online buying from online mexican pharmacy buying prescription drugs in mexico
10yenharwichport.com
남자들은 짐을 꾸리기 시작했고 회계 사무소는 정착하기 시작했습니다.
mexican pharmaceuticals online best online pharmacies in mexico purple pharmacy mexico price list
mexico pharmacy mexican rx online mexican pharmaceuticals online
Hi this is somewhat of off topic but I was wanting to know if blogs use WYSIWYG editors or if you have to manually code with HTML. I’m starting a blog soon but have no coding knowledge so I wanted to get advice from someone with experience. Any help would be enormously appreciated!
purple pharmacy mexico price list mexican border pharmacies shipping to usa best online pharmacies in mexico
ST666
mexican rx online purple pharmacy mexico price list mexico pharmacies prescription drugs
https://mexicanph.com/# reputable mexican pharmacies online
п»їbest mexican online pharmacies
reputable mexican pharmacies online best online pharmacies in mexico reputable mexican pharmacies online
mexico drug stores pharmacies buying prescription drugs in mexico mexican rx online
buying from online mexican pharmacy mexican online pharmacies prescription drugs medication from mexico pharmacy
best online pharmacies in mexico medicine in mexico pharmacies buying from online mexican pharmacy
mexican border pharmacies shipping to usa mexico drug stores pharmacies mexican mail order pharmacies
buying prescription drugs in mexico mexican border pharmacies shipping to usa buying prescription drugs in mexico
buying prescription drugs in mexico mexico pharmacy buying prescription drugs in mexico
https://mexicanph.shop/# buying prescription drugs in mexico
mexico pharmacies prescription drugs
п»їbest mexican online pharmacies mexico drug stores pharmacies best online pharmacies in mexico
buying prescription drugs in mexico mexico pharmacies prescription drugs mexican online pharmacies prescription drugs
mexico pharmacies prescription drugs mexico pharmacy mexican mail order pharmacies
My coder is trying to convince me to move to .net from PHP. I have always disliked the idea because of the costs. But he’s tryiong none the less. I’ve been using WordPress on several websites for about a year and am anxious about switching to another platform. I have heard excellent things about blogengine.net. Is there a way I can import all my wordpress content into it? Any help would be greatly appreciated!
medicine in mexico pharmacies mexican online pharmacies prescription drugs mexico pharmacies prescription drugs
buying from online mexican pharmacy mexican pharmaceuticals online purple pharmacy mexico price list
purple pharmacy mexico price list mexican drugstore online medicine in mexico pharmacies
mexico pharmacies prescription drugs mexico pharmacies prescription drugs reputable mexican pharmacies online
mexico pharmacies prescription drugs buying prescription drugs in mexico best online pharmacies in mexico
mexican online pharmacies prescription drugs mexico pharmacies prescription drugs medicine in mexico pharmacies
mexico pharmacy buying from online mexican pharmacy mexican pharmacy
I and my guys ended up examining the best helpful tips located on your web page while at once got an awful suspicion I never thanked the site owner for those tips. The men were definitely as a result thrilled to read all of them and have extremely been using those things. Many thanks for simply being simply kind and then for opting for varieties of helpful subject matter most people are really desperate to know about. Our own honest apologies for not expressing gratitude to earlier.
https://buyprednisone.store/# prednisone uk buy
generic lisinopril 3973: lisinopril 10 mg tablet – lisinopril 20mg
Its fantastic as your other blog posts : D, regards for posting.
I love it when people come together and share opinions, great blog, keep it up.
Saved as a favorite, I really like your blog!
https://amoxil.cheap/# medicine amoxicillin 500mg
zestril 40 mg: lisinopril 20 mg uk – lisinopril 12.5 mg 10 mg
http://amoxil.cheap/# amoxicillin discount
戰神賽特
2024全新上線❰戰神賽特老虎機❱ – ATG賽特玩法說明介紹
❰戰神賽特老虎機❱是由ATG電子獨家開發的古埃及風格線上老虎機,在傳說中戰神賽特是「力量之神」與奈芙蒂斯女神結成連理,共同守護古埃及的奇幻秘寶,只有被選中的冒險者才能進入探險。
❰戰神賽特老虎機❱ – ATG賽特介紹
2024最新老虎機【戰神塞特】- ATG電子 X 富遊娛樂城
❰戰神賽特老虎機❱ – ATG電子
線上老虎機系統 : ATG電子
發行年分 : 2024年1月
最大倍數 : 51000倍
返還率 : 95.89%
支付方式 : 全盤倍數、消除掉落
最低投注金額 : 0.4元
最高投注金額 : 2000元
可否選台 : 是
可選台台數 : 350台
免費遊戲 : 選轉觸發+購買特色
❰戰神賽特老虎機❱ 賠率說明
戰神塞特老虎機賠率算法非常簡單,玩家們只需要不斷的轉動老虎機,成功消除物件即可贏分,得分賠率依賠率表計算。
當盤面上沒有物件可以消除時,倍數符號將會相加形成總倍數!該次旋轉的總贏分即為 : 贏分 X 總倍數。
積分方式如下 :
贏分=(單次押注額/20) X 物件賠率
EX : 單次押注額為1,盤面獲得12個戰神賽特倍數符號法老魔眼
贏分= (1/20) X 1000=50
以下為各個得分符號數量之獎金賠率 :
得分符號 獎金倍數 得分符號 獎金倍數
戰神賽特倍數符號聖甲蟲 6 2000
5 100
4 60 戰神賽特倍數符號黃寶石 12+ 200
10-11 30
8-9 20
戰神賽特倍數符號荷魯斯之眼 12+ 1000
10-11 500
8-9 200 戰神賽特倍數符號紅寶石 12+ 160
10-11 24
8-9 16
戰神賽特倍數符號眼鏡蛇 12+ 500
10-11 200
8-9 50 戰神賽特倍數符號紫鑽石 12+ 100
10-11 20
8-9 10
戰神賽特倍數符號神箭 12+ 300
10-11 100
8-9 40 戰神賽特倍數符號藍寶石 12+ 80
10-11 18
8-9 8
戰神賽特倍數符號屠鐮刀 12+ 240
10-11 40
8-9 30 戰神賽特倍數符號綠寶石 12+ 40
10-11 15
8-9 5
❰戰神賽特老虎機❱ 賠率說明(橘色數值為獲得數量、黑色數值為得分賠率)
ATG賽特 – 特色說明
ATG賽特 – 倍數符號獎金加乘
玩家們在看到盤面上出現倍數符號時,務必把握機會加速轉動ATG賽特老虎機,倍數符號會隨機出現2到500倍的隨機倍數。
當盤面無法在消除時,這些倍數總和會相加,乘上當時累積之獎金,即為最後得分總額。
倍數符號會出現在主遊戲和免費遊戲當中,玩家們千萬別錯過這個可以瞬間將得獎金額拉高的好機會!
ATG賽特 – 倍數符號獎金加乘
ATG賽特 – 倍數符號圖示
ATG賽特 – 進入神秘金字塔開啟免費遊戲
戰神賽特倍數符號聖甲蟲
❰戰神賽特老虎機❱ 免費遊戲符號
在古埃及神話中,聖甲蟲又稱為「死亡之蟲」,它被當成了天球及重生的象徵,守護古埃及的奇幻秘寶。
當玩家在盤面上,看見越來越多的聖甲蟲時,千萬不要膽怯,只需在牌面上斬殺4~6個ATG賽特免費遊戲符號,就可以進入15場免費遊戲!
在免費遊戲中若轉出3~6個聖甲蟲免費遊戲符號,可額外獲得5次免費遊戲,最高可達100次。
當玩家的累積贏分且盤面有倍數物件時,盤面上的所有倍數將會加入總倍數!
ATG賽特 – 選台模式贏在起跑線
為避免神聖的寶物被盜墓者奪走,富有智慧的法老王將金子塔內佈滿迷宮,有的設滿機關讓盜墓者寸步難行,有的暗藏機關可以直接前往存放神秘寶物的暗房。
ATG賽特老虎機設有350個機檯供玩家選擇,這是連魔龍老虎機、忍老虎機都給不出的機台數量,為的就是讓玩家,可以隨時進入神秘的古埃及的寶藏聖域,挖掘長眠已久的神祕寶藏。
【戰神塞特老虎機】選台模式
❰戰神賽特老虎機❱ 選台模式
ATG賽特 – 購買免費遊戲挖掘秘寶
玩家們可以使用當前投注額的100倍購買免費遊戲!進入免費遊戲再也不是虛幻。獎勵與一般遊戲相同,且購買後遊戲將自動開始,直到場次和獎金發放完畢為止。
有購買免費遊戲需求的玩家們,立即點擊「開始」,啟動神秘金字塔裡的古埃及祕寶吧!
【戰神塞特老虎機】購買特色
❰戰神賽特老虎機❱ 購買特色
sm-slot.com
Zhonglie라는 단어는 날카로운 칼과 같아서 Zhang Sheng의 마음을 꿰뚫고 있습니다.이것은 …이 Zhonglie입니까?
日本にオンラインカジノおすすめランキング2024年最新版
2024おすすめのオンラインカジノ
オンラインカジノはパソコンでしか遊べないというのは、もう一昔前の話。現在はスマホやタブレットなどのモバイル端末からも、パソコンと変わらないクオリティでオンラインカジノを当たり前に楽しむことができるようになりました。
数あるモバイルカジノの中で、当サイトが厳選したトップ5カジノはこちら。
オンラインカジノおすすめ: コニベット(Konibet)
コニベットといえば、キャッシュバックや毎日もらえるリベートボーナスなど豪華ボーナスが満載!それに加えて低い出金条件も見どころです。さらにVIPレベルごとの還元率の高さも業界内で突出している点や、出金速度の速さなどトータルバランスの良さからもハイローラーの方にも好まれています。
カスタマーサポートは365日24時間稼働しているので、初心者の方にも安心してご利用いただけます。
さらに【業界初のオンラインポーカー】を導入!毎日トーナメントも開催されているので、早速参加しちゃいましょう!
RTP(還元率)公開や、入出金対応がスムーズで初心者向き
2000種類以上の豊富なゲーム数を誇り、スロットゲーム多数!
今なら$20の入金不要ボーナスと最大$650還元ボーナス!
8種類以上のライブカジノプロバイダー
業界初オンラインポーカーあり,日本利用者数No.1の安心のオンラインカジノメディア!
おすすめポイント
コニベットは、その豊富なボーナスと高還元率、そして安心のキャッシュバック制度で知られています。まず、新規登録者には入金不要の$20ボーナスが提供され、さらに初回入金時には最大$650の還元ボーナスが得られます。これらのキャンペーンはプレイヤーにとって大きな魅力となっています。
また、コニベットの特徴的な点は、VIP制度です。一度ロイヤルクラブになると、降格がなく、スロットリベートが1.5%という驚異の還元率を享受できます。これは他のオンラインカジノと比較しても非常に高い還元率です。さらに、常時週間損失キャッシュバックも行っているため、不運で負けてしまった場合でも取り返すチャンスがあります。これらの特徴から、コニベットはプレイヤーにとって非常に魅力的なオンラインカジノと言えるでしょう。
コニベット 無料会員登録をする
| コニベットのボーナス
コニベットは、新規登録者向けに20ドルの入金不要ボーナスを用意しています
コニベットカジノでは、限定で初回入金後に残高が1ドル未満になった場合、入金額の50%(最高500ドル)がキャッシュバックされる。キャッシュバック額に出金条件はないため、獲得後にすぐ出金することも可能です。
| コニベットの入金方法
入金方法 最低 / 最高入金
マスターカード 最低 : $20 / 最高 : $6,000
ジェイシービー 最低 : $20/ 最高 : $6,000
アメックス 最低 : $20 / 最高 : $6,000
アイウォレット 最低 : $20 / 最高 : $100,000
スティックペイ 最低 : $20 / 最高 : $100,000
ヴィーナスポイント 最低 : $20 / 最高 : $10,000
仮想通貨 最低 : $20 / 最高 : $100,000
銀行送金 最低 : $20 / 最高 : $10,000
| コニベット出金方法
出金方法 最低 |最高出金
アイウォレット 最低 : $40 / 最高 : なし
スティックぺイ 最低 : $40 / 最高 : なし
ヴィーナスポイント 最低 : $40 / 最高 : なし
仮想通貨 最低 : $40 / 最高 : なし
銀行送金 最低 : $40 / 最高 : なし
buy stromectol canada: stromectol 3 mg price – ivermectin rx
http://buyprednisone.store/# prednisone daily
Hi there! I know this is kinda off topic however I’d figured I’d ask. Would you be interested in exchanging links or maybe guest writing a blog post or vice-versa? My site goes over a lot of the same subjects as yours and I think we could greatly benefit from each other. If you are interested feel free to send me an e-mail. I look forward to hearing from you! Excellent blog by the way!
how much is amoxicillin prescription: amoxil pharmacy – amoxicillin without a prescription
http://furosemide.guru/# furosemide 100 mg
prednisone cost 10mg: prednisone pill 10 mg – prednisone 1 mg tablet
カジノ
日本にオンラインカジノおすすめランキング2024年最新版
2024おすすめのオンラインカジノ
オンラインカジノはパソコンでしか遊べないというのは、もう一昔前の話。現在はスマホやタブレットなどのモバイル端末からも、パソコンと変わらないクオリティでオンラインカジノを当たり前に楽しむことができるようになりました。
数あるモバイルカジノの中で、当サイトが厳選したトップ5カジノはこちら。
オンラインカジノおすすめ: コニベット(Konibet)
コニベットといえば、キャッシュバックや毎日もらえるリベートボーナスなど豪華ボーナスが満載!それに加えて低い出金条件も見どころです。さらにVIPレベルごとの還元率の高さも業界内で突出している点や、出金速度の速さなどトータルバランスの良さからもハイローラーの方にも好まれています。
カスタマーサポートは365日24時間稼働しているので、初心者の方にも安心してご利用いただけます。
さらに【業界初のオンラインポーカー】を導入!毎日トーナメントも開催されているので、早速参加しちゃいましょう!
RTP(還元率)公開や、入出金対応がスムーズで初心者向き
2000種類以上の豊富なゲーム数を誇り、スロットゲーム多数!
今なら$20の入金不要ボーナスと最大$650還元ボーナス!
8種類以上のライブカジノプロバイダー
業界初オンラインポーカーあり,日本利用者数No.1の安心のオンラインカジノメディア!
おすすめポイント
コニベットは、その豊富なボーナスと高還元率、そして安心のキャッシュバック制度で知られています。まず、新規登録者には入金不要の$20ボーナスが提供され、さらに初回入金時には最大$650の還元ボーナスが得られます。これらのキャンペーンはプレイヤーにとって大きな魅力となっています。
また、コニベットの特徴的な点は、VIP制度です。一度ロイヤルクラブになると、降格がなく、スロットリベートが1.5%という驚異の還元率を享受できます。これは他のオンラインカジノと比較しても非常に高い還元率です。さらに、常時週間損失キャッシュバックも行っているため、不運で負けてしまった場合でも取り返すチャンスがあります。これらの特徴から、コニベットはプレイヤーにとって非常に魅力的なオンラインカジノと言えるでしょう。
コニベット 無料会員登録をする
| コニベットのボーナス
コニベットは、新規登録者向けに20ドルの入金不要ボーナスを用意しています
コニベットカジノでは、限定で初回入金後に残高が1ドル未満になった場合、入金額の50%(最高500ドル)がキャッシュバックされる。キャッシュバック額に出金条件はないため、獲得後にすぐ出金することも可能です。
| コニベットの入金方法
入金方法 最低 / 最高入金
マスターカード 最低 : $20 / 最高 : $6,000
ジェイシービー 最低 : $20/ 最高 : $6,000
アメックス 最低 : $20 / 最高 : $6,000
アイウォレット 最低 : $20 / 最高 : $100,000
スティックペイ 最低 : $20 / 最高 : $100,000
ヴィーナスポイント 最低 : $20 / 最高 : $10,000
仮想通貨 最低 : $20 / 最高 : $100,000
銀行送金 最低 : $20 / 最高 : $10,000
| コニベット出金方法
出金方法 最低 |最高出金
アイウォレット 最低 : $40 / 最高 : なし
スティックぺイ 最低 : $40 / 最高 : なし
ヴィーナスポイント 最低 : $40 / 最高 : なし
仮想通貨 最低 : $40 / 最高 : なし
銀行送金 最低 : $40 / 最高 : なし
娛樂城推薦
香港網上賭場
lisinopril 104: lisinopril 25mg tablets – prinivil brand name
http://amoxil.cheap/# amoxicillin where to get
naturally like your website but you have to check the spelling on several of your posts. Many of them are rife with spelling problems and I find it very troublesome to tell the truth nevertheless I’ll certainly come back again.
amoxicillin order online no prescription: buying amoxicillin online – amoxicillin 500 mg for sale
Теневые рынки и их незаконные деятельности представляют существенную угрозу безопасности общества и являются объектом внимания правоохранительных органов по всему миру. В данной статье мы обсудим так называемые теневые рынки, где возможно покупать фальшивые паспорта, и какие угрозы это несет для граждан и государства.
Теневые рынки представляют собой закулисные интернет-площадки, на которых торгуется разнообразной незаконной продукцией и услугами. Среди этих услуг встречается и продажа поддельных удостоверений, таких как личные документы. Эти рынки оперируют в теневой сфере интернета, используя зашифровывание и неизвестные платежные системы, чтобы оставаться непостижимыми для правоохранительных органов.
Покупка нелегального паспорта на теневых рынках представляет значительную угрозу национальной безопасности. похищение личных данных, изготовление фальшивых документов и нелегальные идентификационные материалы могут быть использованы для совершения террористических актов, обмана и прочих преступлений.
Правоохранительные органы в различных странах активно борются с неофициальными рынками, проводя спецоперации по выявлению и задержанию тех, кто замешан в противозаконных операциях. Однако, по мере того как технологии становятся более трудными, эти рынки могут приспосабливаться и находить новые способы обхода законодательства.
Для защиты себя от угроз, связанных с подпольными рынками, важно соблюдать осторожность при обработке своих индивидуальных данных. Это включает в себя остерегаться фишинговых атак, не раскрывать индивидуальной информацией в подозрительных источниках и постоянно проверять свои финансовые документы.
Кроме того, общество должно быть информировано о рисках и последствиях покупки нелегальных документов. Это способствует формированию более осознанного и ответственного подхода к вопросам безопасности и поможет в борьбе с неофициальными рынками. Поддержка законопроектов, направленных на ужесточение наказаний за производство и сбыт нелегальных документов, также представляет важное направление в борьбе с этими преступлениями
http://furosemide.guru/# lasix uses
Magnificent web site. Plenty of helpful info here. I am sending it to several pals ans also sharing in delicious. And certainly, thank you to your sweat!
Wonderful post! We will be linking to this great article on our site.JW Pet Insight Bird Bath Bird Accessory Multicolor Medium – Hot Deals
http://furosemide.guru/# lasix 40 mg
medication lisinopril 20 mg: prinivil 5 mg tablets – order lisinopril 20mg
pragmatic-ko.com
Zhu Houzhao는 “다음에 그 늙은 놈 Zhang Heling을 볼 때 …”라고 짹짹 거리며 콧노래를 불렀습니다.
lisinopril in india: lisinopril for sale online – lisinopril 10 mg price in india
In the realm of premium watches, discovering a dependable source is essential, and WatchesWorld stands out as a pillar of trust and expertise. Providing an broad collection of renowned timepieces, WatchesWorld has collected praise from satisfied customers worldwide. Let’s explore into what our customers are saying about their experiences.
Customer Testimonials:
O.M.’s Review on O.M.:
“Outstanding communication and aftercare throughout the process. The watch was perfectly packed and in pristine condition. I would certainly work with this team again for a watch purchase.”
Richard Houtman’s Review on Benny:
“I dealt with Benny, who was highly supportive and courteous at all times, preserving me regularly informed of the process. Moving forward, even though I ended up acquiring the watch locally, I would still definitely recommend Benny and the company.”
Customer’s Efficient Service Experience:
“A highly efficient and efficient service. Kept me up to date on the order progress.”
Featured Timepieces:
Richard Mille RM30-01 Automatic Winding with Declutchable Rotor:
Price: €285,000
Year: 2023
Reference: RM30-01 TI
Patek Philippe Complications World Time 38.5mm:
Price: €39,900
Year: 2019
Reference: 5230R-001
Rolex Oyster Perpetual Day-Date 36mm:
Price: €76,900
Year: 2024
Reference: 128238-0071
Best Sellers:
Bulgari Serpenti Tubogas 35mm:
Price: On Request
Reference: 101816 SP35C6SDS.1T
Bulgari Serpenti Tubogas 35mm (2024):
Price: €12,700
Reference: 102237 SP35C6SPGD.1T
Cartier Panthere Medium Model:
Price: €8,390
Year: 2023
Reference: W2PN0007
Our Experts Selection:
Cartier Panthere Small Model:
Price: €11,500
Year: 2024
Reference: W3PN0006
Omega Speedmaster Moonwatch 44.25 mm:
Price: €9,190
Year: 2024
Reference: 304.30.44.52.01.001
Rolex Oyster Perpetual Cosmograph Daytona 40mm:
Price: €28,500
Year: 2023
Reference: 116500LN-0002
Rolex Oyster Perpetual 36mm:
Price: €13,600
Year: 2023
Reference: 126000-0006
Why WatchesWorld:
WatchesWorld is not just an web-based platform; it’s a commitment to personalized service in the realm of high-end watches. Our group of watch experts prioritizes trust, ensuring that every customer makes an knowledgeable decision.
Our Commitment:
Expertise: Our group brings exceptional understanding and perspective into the realm of high-end timepieces.
Trust: Trust is the foundation of our service, and we prioritize transparency in every transaction.
Satisfaction: Customer satisfaction is our paramount goal, and we go the extra mile to ensure it.
When you choose WatchesWorld, you’re not just purchasing a watch; you’re investing in a effortless and trustworthy experience. Explore our collection, and let us assist you in discovering the perfect timepiece that embodies your taste and sophistication. At WatchesWorld, your satisfaction is our time-tested commitment
dota2answers.com
사실, 몇몇 제국의 의사들은 이것이 플래시백일까봐 매우 걱정하고 있습니다.
amoxicillin for sale: amoxicillin medicine over the counter – medicine amoxicillin 500mg
You are my aspiration, I possess few blogs and sometimes run out from to post .
https://amoxil.cheap/# amoxicillin online canada
Hello there, You have done an excellent job. I’ll certainly digg it and individually suggest to my friends. I’m sure they will be benefited from this website.
Использование финансовых карт является существенной составляющей современного общества. Карты предоставляют удобство, секретность и разнообразные варианты для проведения финансовых сделок. Однако, кроме легального использования, существует темная сторона — обналичивание карт, когда карты используются для вывода наличных средств без согласия владельца. Это является незаконной практикой и влечет за собой серьезные наказания.
Вывод наличных средств с карт представляет собой практики, направленные на извлечение наличных средств с карты, необходимые для того, чтобы обойти защитные меры и оповещений, предусмотренных банком. К сожалению, такие противозаконные деяния существуют, и они могут привести к финансовым потерям для банков и клиентов.
Одним из способов вывода наличных средств является использование технологических трюков, таких как кража данных с магнитных полос карт. Скимминг — это техника, при котором злоумышленники устанавливают устройства на банкоматах или терминалах оплаты, чтобы считывать информацию с магнитной полосы банковской карты. Полученные данные затем используются для формирования реплики карты или проведения транзакций в интернете.
Другим обычным приемом является ловушка, когда преступники отправляют фальшивые электронные сообщения или создают фейковые сайты, имитирующие банковские ресурсы, с целью сбора конфиденциальных данных от клиентов.
Для предотвращения кэшаута карт банки осуществляют разные действия. Это включает в себя повышение уровня безопасности, введение двухэтапной проверки, слежение за транзакциями и подготовка клиентов о способах предупреждения мошенничества.
Клиентам также следует быть активными в защите своих карт и данных. Это включает в себя регулярное изменение паролей, анализ выписок из банка, а также осторожность по отношению к сомнительным транзакциям.
Вывод наличных средств — это тяжкое преступление, которое причиняет урон не только финансовым учреждениям, но и обществу в целом. Поэтому важно соблюдать бдительность при пользовании банковскими картами, быть осведомленным о методах мошенничества и соблюдать предосторожности для избежания потери денег
http://lisinopril.top/# cost of lisinopril in canada
where to buy amoxicillin pharmacy: amoxicillin 500mg prescription – amoxicillin 500 mg without prescription
lisinopril uk: lisinopril 7.5 mg – lisinopril 10 mg brand name in india
prednisone tablets canada: prednisone 20mg nz – cheap prednisone online
http://buyprednisone.store/# prednisone prescription for sale
lfchungary.com
짧은 시간에 많은 사람들의 손이 더러워졌습니다.
You need to participate in a contest for top-of-the-line blogs on the web. I’ll recommend this site!
mail order pharmacy india reputable indian online pharmacy world pharmacy india
https://indianph.xyz/# online shopping pharmacy india
What i don’t understood is in truth how you’re no longer actually much more well-preferred than you might be right now. You are very intelligent. You realize therefore considerably in relation to this topic, produced me for my part imagine it from so many numerous angles. Its like men and women are not interested unless it is one thing to do with Girl gaga! Your individual stuffs excellent. At all times take care of it up!
Даркнет – это сегмент интернета, которая остается скрытой от обычных поисковых систем и требует специального программного обеспечения для доступа. В этой анонимной зоне сети существует масса ресурсов, включая различные списки и каталоги, предоставляющие доступ к разнообразным услугам и товарам. Давайте рассмотрим, что представляет собой даркнет список и какие тайны скрываются в его глубинах.
Даркнет Списки: Врата в Невидимый Мир
Для начала, что такое даркнет список? Это, по сути, каталоги или индексы веб-ресурсов в темной части интернета, которые позволяют пользователям находить нужные услуги, товары или информацию. Эти списки могут варьироваться от форумов и магазинов до ресурсов, специализирующихся на различных аспектах анонимности и криптовалют.
Категории и Возможности
Черный Рынок:
Даркнет часто ассоциируется с рынком андеграунда, где можно найти различные товары и услуги, включая наркотики, оружие, украденные данные и даже услуги профессиональных устрашителей. Списки таких ресурсов позволяют пользователям без труда находить подобные предложения.
Чаты и Сообщества:
Темная сторона интернета также предоставляет платформы для анонимного общения. Чаты и сообщества на даркнет списках могут заниматься обсуждением тем от кибербезопасности и взлома до политики и философии.
Информационные ресурсы:
Есть ресурсы, предоставляющие информацию и инструкции по обходу цензуры, защите конфиденциальности и другим темам, интересным пользователям, стремящимся сохранить анонимность.
Безопасность и Осторожность
При всей своей анонимности и свободе действий темная сторона интернета также несет риски. Мошенничество, кибератаки и незаконные сделки становятся частью этого мира. Пользователям необходимо проявлять максимальную осторожность и соблюдать меры безопасности при взаимодействии с даркнет списками.
Заключение: Врата в Неизведанный Мир
Даркнет списки предоставляют доступ к теневым уголкам интернета, где сокрыты тайны и возможности. Однако, как и в любой неизведанной территории, важно помнить о возможных рисках и осознанно подходить к использованию темной стороны интернета. Анонимность не всегда гарантирует безопасность, и путешествие в этот мир требует особой осторожности и знания.
Независимо от того, интересуетесь ли вы техническими аспектами интернет-безопасности, ищете уникальные товары или просто исследуете новые грани интернета, даркнет списки предоставляют ключ
Даркнет – таинственная зона всемирной паутины, избегающая взоров обычных поисковых систем и требующая дополнительных средств для доступа. Этот скрытый ресурс сети обильно насыщен сайтами, предоставляя доступ к разнообразным товарам и услугам через свои даркнет списки и каталоги. Давайте ближе рассмотрим, что представляют собой эти списки и какие тайны они сокрывают.
Даркнет Списки: Окна в Неизведанный Мир
Индексы веб-ресурсов в темной части интернета – это вид проходы в неощутимый мир интернета. Перечни и указатели веб-ресурсов в даркнете, они позволяют пользователям отыскивать разнообразные услуги, товары и информацию. Варьируя от форумов и магазинов до ресурсов, уделяющих внимание аспектам анонимности и криптовалютам, эти списки предоставляют нам шанс заглянуть в таинственный мир даркнета.
Категории и Возможности
Теневой Рынок:
Даркнет часто связывается с теневым рынком, где доступны разнообразные товары и услуги – от наркотических препаратов и стрелкового вооружения до украденных данных и услуг наемных убийц. Списки ресурсов в этой категории облегчают пользователям находить подходящие предложения без лишних усилий.
Форумы и Сообщества:
Даркнет также предоставляет площадку для анонимного общения. Форумы и сообщества, указанные в каталогах даркнета, охватывают различные темы – от компьютерной безопасности и хакерских атак до политических аспектов и философских концепций.
Информационные Ресурсы:
На даркнете есть ресурсы, предоставляющие сведения и руководства по преодолению цензуры, обеспечению конфиденциальности и другим темам, интересным тем, кто хочет сохранить свою конфиденциальность.
Безопасность и Осторожность
Несмотря на неизвестность и свободу, даркнет полон рисков. Мошенничество, кибератаки и незаконные сделки присущи этому миру. Взаимодействуя с списками ресурсов в темной сети, пользователи должны соблюдать максимальную осторожность и придерживаться мер безопасности.
Заключение
Списки даркнета – это путь в неизведанный мир, где сокрыты тайны и возможности. Однако, как и в любой неизведанной территории, путешествие в темную сеть требует особой осторожности и знания. Анонимность не всегда гарантирует безопасность, и использование даркнета требует осознанного подхода. Независимо от ваших интересов – будь то технические детали в области кибербезопасности, поиск необычных товаров или исследование новых возможностей в интернете – реестры даркнета предоставляют ключ
lfchungary.com
친애하는 책 친구 여러분, 이 책은 서가에 올려진 이후로 거의 250만 단어를 담고 있습니다.
I really enjoy studying on this site, it contains great blog posts. “Never fight an inanimate object.” by P. J. O’Rourke.
https://indianph.com/# indian pharmacy
http://indianph.com/# online pharmacy india
online shopping pharmacy india
I like the valuable information you provide in your articles. I’ll bookmark your weblog and check again here frequently. I’m quite certain I will learn plenty of new stuff right here! Best of luck for the next!
casino
I’m now not sure where you are getting your information, but good topic. I must spend some time learning much more or working out more. Thank you for great info I was looking for this info for my mission.
This is a topic close to my heart cheers, where are your contact details though?
cipro pharmacy: ciprofloxacin 500 mg tablet price – buy generic ciprofloxacin
pragmatic-ko.com
Zhu Biaozhen은 매우 어렸고 둘째 아들이었고 그는 현 왕자 만 계승했습니다.
https://diflucan.pro/# order diflucan
should i take tamoxifen: where to buy nolvadex – tamoxifen benefits
As I web-site possessor I believe the content matter here is rattling fantastic , appreciate it for your hard work. You should keep it up forever! Good Luck.
Nice post. I was checking continuously this blog and I’m impressed! Extremely helpful information particularly the last part 🙂 I care for such information a lot. I was looking for this certain information for a very long time. Thank you and best of luck.
tamoxifen hot flashes: tamoxifen for breast cancer prevention – lexapro and tamoxifen
Thanks a lot for sharing this with all of us you actually know what you are talking about! Bookmarked. Kindly also visit my web site =). We could have a link exchange contract between us!
I conceive you have remarked some very interesting points, regards for the post.
It’s hard to find knowledgeable people on this topic, but you sound like you know what you’re talking about! Thanks
http://cytotec24.shop/# buy cytotec online
https://diflucan.pro/# diflucan 150 mg tablet
Good post. I study something more difficult on totally different blogs everyday. It should at all times be stimulating to read content material from different writers and practice a bit of one thing from their store. I’d want to make use of some with the content on my weblog whether you don’t mind. Natually I’ll offer you a link in your web blog. Thanks for sharing.
Undeniably believe that which you said. Your favorite reason appeared to be on the net the easiest thing to be aware of. I say to you, I certainly get annoyed while people consider worries that they just do not know about. You managed to hit the nail upon the top as well as defined out the whole thing without having side effect , people could take a signal. Will probably be back to get more. Thanks
buy cytotec pills online cheap: cytotec buy online usa – cytotec buy online usa
заливы без предоплат
В последнее период становятся известными запросы о заливах без предварительной оплаты – услугах, предоставляемых в сети, где клиентам обещают выполнение задачи или предоставление услуги перед оплаты. Однако, за данной кажущейся возможностью могут прятаться значительные риски и негативные последствия.
Привлекательная сторона безоплатных заливов:
Привлекательная сторона концепции заливов без предварительной оплаты заключается в том, что клиенты получают сервис или продукцию, не выплачивая первоначально деньги. Это может показаться выгодным и удобным, в частности для тех, кто не хочет ставить под риск деньгами или остаться обманутым. Однако, до того как вовлечься в сферу безоплатных переводов, следует принять во внимание несколько важных аспектов.
Риски и негативные последствия:
Мошенничество и недобросовестные действия:
За честными предложениями без предварительной оплаты могут скрываться мошеннические схемы, приготовленные использовать уважение потребителей. Попав в их ловушку, вы можете лишиться не только это, услуги финансов.
Сниженное качество выполнения услуг:
Без обеспечения оплаты исполнителю может быть недостаточно стимула предоставить высококачественную работу или товар. В результате заказчик останется недовольным, а исполнитель не подвергнется серьезными санкциями.
Утрата данных и безопасности:
При предоставлении личных сведений или информации о банковских счетах для безоплатных переводов существует риск утечки информации и последующего ихнего неправомерного использования.
Рекомендации по безопасным переводам:
Исследование:
Перед подбором бесплатных переводов осуществите комплексное исследование исполнителя. Мнения, рейтинги и репутация могут быть полезным показателем.
Предоплата:
Если возможно, старайтесь согласовать определенный процент оплаты вперед. Это может сделать соглашение более защищенной и гарантирует вам больший управления.
Достоверные платформы:
Предпочитайте использованию проверенных площадок и сервисов для заливов. Такой выбор уменьшит риск обмана и повысит шансы на получение наилучших качественных услуг.
Итог:
Не смотря на видимую привлекательность, безвозмездные переводы без предварительной оплаты несут в себе риски и потенциальные опасности. Осторожность и осмотрительность при выборе исполнителя или сервиса способны предупредить негативные ситуации. Важно запомнить, что безоплатные переводы могут стать причиной затруднений, и разумное принятие решений способствует предотвратить потенциальных неприятностей
даркнет новости
Теневая зона – это таинственная и непознанная территория интернета, где действуют свои правила, возможности и опасности. Каждый день в мире теневой сети происходят события, о которых обычные участники могут только подозревать. Давайте изучим актуальные сведения из теневой зоны, отражающие современные тенденции и инциденты в этом таинственном уголке сети.”
Тенденции и События:
“Эволюция Технологий и Безопасности:
В даркнете непрерывно развиваются технологии и методы обеспечения безопасности. Новости о внедрении улучшенных платформ шифрования, анонимизации и защиты личных данных говорят о стремлении пользователей и специалистов к обеспечению надежной среды.”
“Свежие Теневые Рынки:
В соответствии с динамикой спроса и предложений, в теневом интернете появляются совершенно новые коммерческие площадки. Информация о открытии цифровых рынков предоставляют участникам различные варианты для купли-продажи продукцией и услугами
lfchungary.com
Hongzhi 황제는 입술을 깨물고 소리를 내지 않고 묵인했습니다.
даркнет 2024
Даркнет 2024: Неявные аспекты цифровой среды
С начала даркнет представлял собой сферу веба, где секретность и тень были нормой. В 2024 году этот непрозрачный мир продолжает, предоставляя новые вызовы и опасности для сообщества в сети. Рассмотрим, какими тенденции и изменения ожидают нас в даркнете 2024.
Продвижение технологий и Повышение скрытности
С прогрессом технологий, инструменты для обеспечения скрытности в теневом интернете становятся сложнее и эффективными. Использование криптовалют, современных шифровальных методов и децентрализованных сетей делает слежение за поведением участников еще более трудным для силовых структур.
Развитие тематических рынков
Темные рынки, специализирующиеся на разнообразных продуктах и сервисах, продолжают расширяться. Наркотики, оружие, хакерские инструменты, краденые данные – ассортимент продукции становится все разнообразным. Это порождает вызов для правопорядка, стоящего перед необходимостью адаптироваться к изменяющимся сценариям преступной деятельности.
Опасности цифровой безопасности для обычных пользователей
Сервисы аренды хакерских услуг и мошеннические схемы остаются активными в даркнете. Люди, не связанные с преступностью попадают в руки объектом для преступников в сети, стремящихся зайти к персональной информации, счетам в банке и другой конфиденциальной информации.
Возможности цифровой реальности в даркнете
С прогрессом техники цифровой симуляции, теневой интернет может перейти в новый этап, предоставляя пользователям реальные и вовлекающие виртуальные пространства. Это может сопровождаться дополнительными видами нелегальных действий, такими как виртуальные торговые площадки для передачи цифровыми товарами.
Борьба силам защиты
Силы безопасности совершенствуют свои технические средства и методы противостояния даркнетом. Совместные усилия стран и международных организаций ориентированы на профилактику цифровой преступности и противостояние современным проблемам, которые возникают в связи с развитием темного интернета.
Заключение
Теневой интернет в 2024 году остается сложной и многогранной обстановкой, где технические инновации продвигаются вносить изменения в пейзаж нелегальных действий. Важно для участников продолжать быть бдительными, гарантировать свою защиту в интернете и следовать нормы, даже при нахождении в цифровой среде. Вместе с тем, противостояние с теневым интернетом требует совместных усилиях от стран, технологических компаний и граждан, чтобы обеспечить безопасность в цифровом мире.
sm-casino1.com
“…” Fang Jifan은 갑자기 자신의 캐릭터에 대해 극도의 자신감을 갖게 되었습니다.
https://cipro.guru/# cipro
http://doxycycline.auction/# cheap doxycycline online
Thanks for another great article. Where else may anybody get that kind of information in such a perfect approach of writing? I have a presentation subsequent week, and I am at the search for such information.
doxycycline generic doxy doxycycline 100 mg
I’m still learning from you, but I’m making my way to the top as well. I definitely enjoy reading everything that is posted on your blog.Keep the aarticles coming. I loved it!
mikschai.com
Hongzhi 황제는 고개를 끄덕였지만 핵심 정보를 파악하고 서둘러 물었다.
winbet casino
http://cipro.guru/# ciprofloxacin 500mg buy online
I’m extremely impressed together with your writing talents and also with the format in your weblog. Is this a paid topic or did you customize it yourself? Anyway stay up the nice high quality writing, it is uncommon to see a great blog like this one nowadays..
https://cytotec24.shop/# buy cytotec in usa
Взлом Telegram: Мифы и Реальность
Телеграм – это популярный мессенджер, отмеченный своей превосходной степенью кодирования и защиты данных пользователей. Однако, в современном цифровом мире тема взлома Telegram периодически поднимается. Давайте рассмотрим, что на самом деле стоит за этим понятием и почему нарушение Телеграм чаще является фантазией, чем реальностью.
Кодирование в Телеграм: Основные принципы Безопасности
Телеграм известен своим превосходным уровнем кодирования. Для обеспечения конфиденциальности переписки между участниками используется протокол MTProto. Этот протокол обеспечивает полное кодирование, что означает, что только отправитель и получатель могут понимать сообщения.
Легенды о Взломе Telegram: Почему они появляются?
В последнее время в сети часто появляются утверждения о нарушении Telegram и доступе к персональной информации пользователей. Однако, основная часть этих утверждений оказываются неточными данными, часто возникающими из-за недопонимания принципов работы мессенджера.
Кибернападения и Раны: Фактические Угрозы
Хотя взлом Телеграма в большинстве случаев является трудной задачей, существуют актуальные опасности, с которыми сталкиваются пользователи. Например, кибератаки на индивидуальные аккаунты, вредоносные программы и прочие методы, которые, тем не менее, требуют в активном участии пользователя в их распространении.
Защита Личной Информации: Советы для Участников
Несмотря на отсутствие конкретной опасности нарушения Telegram, важно соблюдать основные правила кибербезопасности. Регулярно обновляйте приложение, используйте двухэтапную проверку, избегайте сомнительных ссылок и мошеннических атак.
Итог: Фактическая Угроза или Излишняя беспокойство?
Взлом Telegram, как обычно, оказывается неоправданным страхом, созданным вокруг темы разговора без явных доказательств. Однако безопасность всегда остается приоритетом, и участники мессенджера должны быть бдительными и следовать советам по обеспечению безопасности своей личной информации
Взлом WhatsApp: Фактичность и Мифы
WhatsApp – один из известных мессенджеров в мире, массово используемый для обмена сообщениями и файлами. Он известен своей кодированной системой обмена данными и гарантированием конфиденциальности пользователей. Однако в интернете время от времени возникают утверждения о возможности взлома WhatsApp. Давайте разберемся, насколько эти утверждения соответствуют фактичности и почему тема нарушения Вотсап вызывает столько дискуссий.
Кодирование в WhatsApp: Охрана Личной Информации
WhatsApp применяет end-to-end шифрование, что означает, что только передающая сторона и получатель могут понимать сообщения. Это стало фундаментом для уверенности многих пользователей мессенджера к сохранению их личной информации.
Легенды о Нарушении Вотсап: Почему Они Появляются?
Интернет периодически заполняют слухи о взломе Вотсап и возможном доступе к переписке. Многие из этих утверждений порой не имеют оснований и могут быть результатом паники или дезинформации.
Фактические Угрозы: Кибератаки и Безопасность
Хотя нарушение WhatsApp является трудной задачей, существуют актуальные угрозы, такие как кибератаки на отдельные аккаунты, фишинг и вредоносные программы. Исполнение мер охраны важно для минимизации этих рисков.
Защита Личной Информации: Рекомендации Пользователям
Для укрепления охраны своего аккаунта в WhatsApp пользователи могут использовать двухфакторную аутентификацию, регулярно обновлять приложение, избегать сомнительных ссылок и следить за конфиденциальностью своего устройства.
Заключение: Реальность и Осторожность
Взлом WhatsApp, как обычно, оказывается трудным и маловероятным сценарием. Однако важно помнить о реальных угрозах и принимать меры предосторожности для защиты своей личной информации. Исполнение рекомендаций по охране помогает поддерживать конфиденциальность и уверенность в использовании мессенджера
tamoxifen hip pain nolvadex for sale tamoxifen moa
https://nolvadex.guru/# tamoxifen bone pain
Thanks, I have recently been looking for info about this subject for ages and yours is the greatest I have found out till now. However, what about the conclusion? Are you sure about the supply?
pragmatic-ko.com
Ouyang Zhi는 천천히 일어나 경례했습니다. “장관이 여기 있습니다.”
You made some decent points there. I looked on the internet for the issue and found most individuals will consent with your blog.
whoah this blog is fantastic i love reading your articles. Keep up the great work! You know, a lot of people are hunting around for this info, you could help them greatly.
Angela White filmleri: Angela Beyaz modeli – Angela Beyaz modeli
https://angelawhite.pro/# Angela White filmleri
sweety fox: Sweetie Fox video – Sweetie Fox video
Selamat datang di situs kantorbola , agent judi slot gacor terbaik dengan RTP diatas 98% , segera daftar di situs kantor bola untuk mendapatkan bonus deposit harian 100 ribu dan bonus rollingan 1%
?????? ????: Angela White izle – Angela Beyaz modeli
http://lanarhoades.fun/# lana rhoades modeli
http://sweetiefox.online/# Sweetie Fox modeli
http://sweetiefox.online/# sweeti fox
Angela White: Angela White – Angela White
http://evaelfie.pro/# eva elfie modeli
eva elfie video: eva elfie modeli – eva elfie izle
http://abelladanger.online/# abella danger filmleri
http://lanarhoades.fun/# lana rhoades video
pragmatic-ko.com
Zhu Houzhao는 이빨을 드러내며 “무슨 소리야? “라고 말했습니다.
https://evaelfie.pro/# eva elfie izle
Nice post. I learn one thing more difficult on completely different blogs everyday. It will at all times be stimulating to learn content material from different writers and apply a little bit something from their store. I’d favor to use some with the content on my weblog whether you don’t mind. Natually I’ll offer you a hyperlink on your net blog. Thanks for sharing.
Woh I like your content, bookmarked! .
?????? ????: Angela White filmleri – Angela White
https://angelawhite.pro/# Angela White
https://evaelfie.pro/# eva elfie video
https://lanarhoades.fun/# lana rhoades video
lana rhoades: lana rhoades – lana rhoades filmleri
sm-online-game.com
“아야.” 왕진위안은 무의식적으로 공중제비를 돌렸다.
http://evaelfie.pro/# eva elfie
Hello my loved one! I want to say that this post is awesome, nice written and include almost all important infos. I¦d like to peer extra posts like this .
Good website! I truly love how it is simple on my eyes and the data are well written. I am wondering how I might be notified when a new post has been made. I have subscribed to your RSS feed which must do the trick! Have a great day!
Hiya, I’m really glad I have found this info. Nowadays bloggers publish only about gossips and web and this is actually irritating. A good blog with exciting content, this is what I need. Thank you for keeping this web site, I’ll be visiting it. Do you do newsletters? Can’t find it.
With havin so much written content do you ever run into any issues of plagorism or copyright violation? My site has a lot of completely unique content I’ve either created myself or outsourced but it seems a lot of it is popping it up all over the internet without my agreement. Do you know any ways to help reduce content from being ripped off? I’d certainly appreciate it.
http://angelawhite.pro/# Angela White
https://sweetiefox.online/# Sweetie Fox
I enjoy the efforts you have put in this, thank you for all the great content.
Nice read, I just passed this onto a colleague who was doing some research on that. And he just bought me lunch since I found it for him smile Thus let me rephrase that: Thanks for lunch!
Outstanding post, you have pointed out some excellent details , I besides think this s a very great website.
http://evaelfie.pro/# eva elfie izle
?????? ????: Abella Danger – abella danger filmleri
http://evaelfie.pro/# eva elfie izle
http://abelladanger.online/# abella danger video
Hiya very nice blog!! Guy .. Excellent .. Amazing .. I will bookmark your website and take the feeds also?KI am satisfied to search out so many useful information right here within the submit, we need develop more techniques on this regard, thank you for sharing. . . . . .
Angela White izle: ?????? ???? – ?????? ????
http://evaelfie.site/# eva elfie new video
bistroduet.com
Hongzhi 황제는 “Xishan에서 이와 같은 작업장을 더 많이 만들어야합니다 …”라고 말했습니다.
Thanks , I have just been searching for information approximately this topic for a long time and yours is the best I have discovered so far. However, what about the bottom line? Are you certain about the supply?
фальшивые 5000 купитьФальшивые купюры 5000 рублей: Опасность для экономики и граждан
Фальшивые купюры всегда были важной угрозой для финансовой стабильности общества. В последние годы одним из ключевых объектов манипуляций стали банкноты номиналом 5000 рублей. Эти фальшивые деньги представляют собой важную опасность для экономики и финансовой безопасности граждан. Давайте рассмотрим, почему фальшивые купюры 5000 рублей стали существенной бедой.
Сложностью выявления.
Купюры 5000 рублей являются самыми крупными по номиналу, что делает их чрезвычайно привлекательными для фальшивомонетчиков. Превосходно проработанные подделки могут быть затруднительно выявить даже специалистам в сфере финансов. Современные технологии позволяют создавать превосходные копии с использованием новейших методов печати и защитных элементов.
Риск для бизнеса.
Фальшивые 5000 рублей могут привести к крупным финансовым убыткам для предпринимателей и компаний. Бизнесы, принимающие наличные средства, становятся подвергаются риску принять фальшивую купюру, что в конечном итоге может снизить прибыль и повлечь за собой юридические последствия.
Повышение инфляции.
Фальшивые деньги увеличивают количество в обращении, что в свою очередь может привести к инфляции. Рост количества контрафактных купюр создает дополнительный денежный объем, не обеспеченный реальными товарами и услугами. Это может существенно подорвать доверие к национальной валюте и стимулировать рост цен.
Вред для доверия к финансовой системе.
Фальшивые деньги вызывают мизерию к финансовой системе в целом. Когда люди сталкиваются с риском получить фальшивые купюры при каждой сделке, они становятся более склонными избегать использования наличных средств, что может привести к обострению проблем, связанных с электронными платежами и банковскими системами.
Защитные меры и образование.
Для борьбы с распространению фальшивых денег необходимо внедрять более совершенные защитные меры на банкнотах и активно проводить просветительскую работу среди населения. Гражданам нужно быть более внимательными при приеме наличных средств и обучаться основам распознавания фальшивых купюр.
В заключение:
Фальшивые купюры 5000 рублей представляют серьезную угрозу для финансовой стабильности и безопасности граждан. Необходимо активно внедрять новые технологии защиты и проводить информационные кампании, чтобы общество было лучше осведомлено о методах распознавания и защиты от фальшивых денег. Только совместные усилия банков, правоохранительных органов и общества в целом позволят минимизировать угрозу подделок и обеспечить стабильность финансовой системы.
mia malkova: mia malkova full video – mia malkova movie
catholic christian dating website: http://miamalkova.life/# mia malkova movie
sweetie fox full: sweetie fox cosplay – sweetie fox full video
https://sweetiefox.pro/# sweetie fox cosplay
twichclip.com
이대로 계속 올라가면 언제쯤에 살만한 큰집이 생길까요?
eva elfie new videos: eva elfie – eva elfie videos
hoki1881
mia malkova movie: mia malkova – mia malkova only fans
chutneyb.com
“두렵지 않다.” Zhu Houzhao가 의기양양하게 말했다. “아이스크림과 똑같습니다.”
где купить фальшивые деньги
Фальшивые деньги: угроза для финансовой системы и общества
Введение:
Фальшивомонетничество – нарушение, оставшееся актуальным на продолжительностью многих веков. Производство и распространение фальшивых денег представляют серьезную угрозу не только для экономической системы, но и для общественной стабильности. В данной статье мы рассмотрим масштабы проблемы, методы борьбы с фальшивомонетничеством и воздействие для социума.
История поддельных купюр:
Фальшивые деньги существуют с момента появления самой концепции денег. В древности подделывались металлические монеты, а в наше время преступники активно используют передовые технологии для фальсификации банкнот. Развитие цифровых технологий также открыло дополнительные способы для создания электронных аналогов денег.
Масштабы проблемы:
Ненастоящая валюта создают угрозу для стабильности экономики. Банки, компании и даже простые люди могут стать пострадавшими обмана. Рост количества поддельных купюр может привести к потере покупательной способности и даже к экономическим кризисам.
Современные методы подделки:
С прогрессом техники подделка стала более затруднительной и изощренной. Преступники используют высокотехнологичное оборудование, профессиональные печатающие устройства, и даже машинное обучение для создания невозможно отличить поддельные копии от оригинальных денежных средств.
Борьба с подделкой денег:
Государства и центральные банки активно внедряют современные методы для предотвращения фальшивомонетничества. Это включает в себя использование современных защитных элементов на банкнотах, просвещение граждан методам распознавания поддельных денег, а также сотрудничество с правоохранительными органами для выявления и предотвращения криминальных группировок.
Последствия для социума:
Фальшивые деньги несут не только экономические, но и социальные последствия. Граждане и бизнесы теряют доверие к финансовой системе, а борьба с криминальной деятельностью требует больших затрат, которые могли бы быть направлены на более полезные цели.
Заключение:
Фальшивые деньги – серьезная проблема, требующая уделяемого внимания и совместных усилий общества, правоохранительных органов и учреждений финансов. Только путем эффективной борьбы с нарушением можно обеспечить стабильность экономики и сохранить доверие к валютной системе
http://evaelfie.site/# eva elfie
ST666️ – Trang Chủ Chính Thức Số 1️⃣ Của Nhà Cái ST666
ST666 đã nhanh chóng trở thành điểm đến giải trí cá độ thể thao được yêu thích nhất hiện nay. Mặc dù chúng tôi mới xuất hiện trên thị trường cá cược trực tuyến Việt Nam gần đây, nhưng đã nhanh chóng thu hút sự quan tâm của cộng đồng người chơi trực tuyến. Đối với những người yêu thích trò chơi trực tuyến, nhà cái ST666 nhận được sự tin tưởng và tín nhiệm trọn vẹn từ họ. ST666 được coi là thiên đường cho những người chơi tham gia.
Giới Thiệu Nhà Cái ST666
ST666.BLUE – ST666 là nơi cá cược đổi thưởng trực tuyến được ưa chuộng nhất hiện nay. Tham gia vào trò chơi cá cược trực tuyến, người chơi không chỉ trải nghiệm các trò giải trí hấp dẫn mà còn có cơ hội nhận các phần quà khủng thông qua các kèo cá độ. Với những phần thưởng lớn, người chơi có thể thay đổi cuộc sống của mình.
Giới Thiệu Nhà Cái ST666 BLUE
Thông tin về nhà cái ST666
ST666 là Gì?
Nhà cái ST666 là một sân chơi cá cược đổi thưởng trực tuyến, chuyên cung cấp các trò chơi cá cược đổi thưởng có thưởng tiền mặt. Điều này bao gồm các sản phẩm như casino, bắn cá, thể thao, esports… Người chơi có thể tham gia nhiều trò chơi hấp dẫn khi đăng ký, đặt cược và có cơ hội nhận thưởng lớn nếu chiến thắng hoặc mất số tiền cược nếu thất bại.
Nhà Cái ST666 – Sân Chơi Cá Cược An Toàn
Nhà Cái ST666 – Sân Chơi Cá Cược Trực Tuyến
Nguồn Gốc Thành Lập Nhà Cái ST666
Nhà cái ST666 được thành lập và ra mắt vào năm 2020 tại Campuchia, một quốc gia nổi tiếng với các tập đoàn giải trí cá cược đổi thưởng. Xuất hiện trong giai đoạn phát triển mạnh mẽ của ngành cá cược, ST666 đã để lại nhiều dấu ấn. Được bảo trợ tài chính bởi tập đoàn danh tiếng Venus Casino, thương hiệu đã mở rộng hoạt động khắp Đông Nam Á và lan tỏa sang cả các quốc gia Châu Á, bao gồm cả Trung Quốc
gambling 7d54acd
Excellent web site. A lot of useful info here. I am sending it to several friends ans additionally sharing in delicious. And obviously, thank you for your sweat!
lana rhoades solo: lana rhoades boyfriend – lana rhoades solo
mia malkova: mia malkova videos – mia malkova latest
http://lanarhoades.pro/# lana rhoades hot
jelenakaludjerovic.com
Liang Ruying은 차에 앉아 있었고 그녀와 함께 한 사람은 또 다른 급우였습니다.
ph sweetie fox: sweetie fox full video – sweetie fox full
https://evaelfie.site/# eva elfie full video
meet singles online: https://miamalkova.life/# mia malkova latest
DNABET
เว็บไซต์ DNABET: สู่ ประสบการณ์ การแทง ที่ไม่เป็นไปตาม ที่คุณ เคย ประสบ!
DNABET ยังคง เป็น เลือกที่คนนิยม สำหรับคน สาวก การพนัน ทางอินเทอร์เน็ต ในประเทศไทย นี้.
ไม่ต้อง เสียเวลา ในการเลือกว่าจะ แข่ง DNABET เพราะที่นี่คือที่ที่ ไม่ต้อง เลือกที่จะ จะได้ หรือไม่ได้รับ!
DNABET มีค่า การชำระเงิน ทุกราคา หวย สูง ตั้งแต่ 900 บาท ขึ้นไป เมื่อ ทุกท่าน ถูกรางวัล ได้รับ รางวัลมากมาย กว่า เว็บ ๆ ที่ เคย.
นอกจากนี้ DNABET ยังคง มีความหลากหลาย หวย ที่คุณสามารถทำการเลือก มากถึง 20 หวย ทั่วโลกนี้ ทำให้คุณสามารถ เลือกเล่น ตามใจต้องการ ได้อย่างหลากหลายแบบ.
ไม่ว่าจะเป็น หวยรัฐ หุ้น ยี่กี หวยฮานอย ลาว และ ลอตเตอรี่รางวัลที่ มีค่า เพียง 80 บาท.
ทาง DNABET มั่นคง ในเรื่องการเงิน โดย ได้ เปลี่ยนชื่อ ชันเจน เป็น DNABET เพื่อ เสริมฐานลูกค้า และ ปรับปรุงระบบให้ สะดวกสบายมาก ขึ้น.
นอกจากนี้ DNABET ยังมี โปรโมชั่น ให้เลือก มากมาย เช่นเดียวกับ โปรโมชั่น สมาชิกใหม่ที่ ท่านสมัคร ในวันนี้ จะได้รับ โบนัสเพิ่ม 500 บาท หรือเครดิตทดลอง ไม่ต้อง เงิน.
นอกจากนี้ DNABET ยังมี ประจำเดือนที่ ท่าน และ DNABET เป็นทางเลือก การเล่น หวย ของท่านเอง พร้อม โปรโมชั่น และ เหล่าโปรโมชั่น ที่ เยอะ ที่สุด ปี 2024.
อย่า ปล่อย โอกาสที่ดีนี้ ไป มาเป็นส่วนหนึ่งของ DNABET และ เพลิดเพลินกับ ประสบการณ์การเล่น การเดิมพันที่ไม่เหมือนใคร ทุกท่าน มีโอกาสที่จะ เป็นเศรษฐี ได้รับ เพียง แค่ เลือก DNABET เว็บแทงหวย ออนไลน์ ที่มั่นใจ และ มีสมาชิกมากที่สุด ในประเทศไทย!
mia malkova videos: mia malkova latest – mia malkova movie
Thanks for another informative web site. Where else could I get that type of information written in such a perfect way? I have a project that I am just now working on, and I’ve been on the look out for such information.
mia malkova: mia malkova – mia malkova movie
http://miamalkova.life/# mia malkova hd
lana rhoades full video: lana rhoades hot – lana rhoades hot
I’ve read some excellent stuff here. Definitely worth bookmarking for revisiting. I wonder how much attempt you set to make the sort of great informative website.
1881
raytalktech.com
일반적으로 향후 실제 기록의 수정이 아니라면 아무도 신경 쓰지 않을 것입니다.
Hello, you used to write fantastic, but the last several posts have been kinda boring… I miss your tremendous writings. Past few posts are just a little bit out of track! come on!
eva elfie hot: eva elfie hot – eva elfie photo
https://evaelfie.site/# eva elfie
Hi are using WordPress for your blog platform? I’m new to the blog world but I’m trying to get started and create my own. Do you require any coding expertise to make your own blog? Any help would be greatly appreciated!
sweetie fox cosplay: sweetie fox full – sweetie fox cosplay
smcasino-game.com
Fang Jifan은 “아직 시간이 있으니 열심히해야합니다. “라고 손가락을 세었습니다.
https://sweetiefox.pro/# sweetie fox full video
I haven’t checked in here for a while as I thought it was getting boring, but the last several posts are great quality so I guess I’ll add you back to my everyday bloglist. You deserve it my friend 🙂
http://sweetiefox.pro/# ph sweetie fox
manzanaresstereo.com
자(子)의 때, 새해, 홍지(洪志) 12년이 시작되었다.
situs kantorbola
KANTORBOLA situs gamin online terbaik 2024 yang menyediakan beragam permainan judi online easy to win , mulai dari permainan slot online , taruhan judi bola , taruhan live casino , dan toto macau . Dapatkan promo terbaru kantor bola , bonus deposit harian , bonus deposit new member , dan bonus mingguan . Kunjungi link kantorbola untuk melakukan pendaftaran .
Some really excellent info Sword lily I detected this. – hey dudes for men
jbustinphoto.com
Xu Pengju는 그의 얼굴에 두려움의 흔적없이 그렇게 대담하게 떠났습니다.
lana rhoades hot: lana rhoades pics – lana rhoades boyfriend
eva elfie new videos: eva elfie photo – eva elfie hot
http://sweetiefox.pro/# sweetie fox new
mia malkova videos: mia malkova hd – mia malkova videos
single website: https://lanarhoades.pro/# lana rhoades pics
http://sweetiefox.pro/# sweetie fox new
https://jogodeaposta.fun/# jogo de aposta online
aviator oyunu: pin up aviator – aviator oyna
Login Ngamenjitu
Portal Judi: Situs Togel Daring Terbesar dan Terjamin
Portal Judi telah menjadi salah satu portal judi online terbesar dan terpercaya di Indonesia. Dengan beragam market yang disediakan dari Semar Group, Portal Judi menawarkan sensasi bermain togel yang tak tertandingi kepada para penggemar judi daring.
Pasaran Terunggul dan Terpenuhi
Dengan total 56 market, Situs Judi menampilkan berbagai opsi terbaik dari pasaran togel di seluruh dunia. Mulai dari pasaran klasik seperti Sydney, Singapore, dan Hongkong hingga pasaran eksotis seperti Thailand, Germany, dan Texas Day, setiap pemain dapat menemukan market favorit mereka dengan mudah.
Langkah Main yang Praktis
Situs Judi menyediakan panduan cara bermain yang mudah dipahami bagi para pemula maupun penggemar togel berpengalaman. Dari langkah-langkah pendaftaran hingga penarikan kemenangan, semua informasi tersedia dengan jelas di situs Portal Judi.
Rekapitulasi Terkini dan Info Terkini
Pemain dapat mengakses hasil terakhir dari setiap pasaran secara real-time di Portal Judi. Selain itu, informasi terkini seperti jadwal bank daring, gangguan, dan offline juga disediakan untuk memastikan kelancaran proses transaksi.
Bermacam-macam Jenis Game
Selain togel, Portal Judi juga menawarkan bervariasi jenis permainan kasino dan judi lainnya. Dari bingo hingga roulette, dari dragon tiger hingga baccarat, setiap pemain dapat menikmati bervariasi pilihan permainan yang menarik dan menghibur.
Keamanan dan Kepuasan Pelanggan Terjamin
Situs Judi mengutamakan security dan kepuasan pelanggan. Dengan sistem security terbaru dan layanan pelanggan yang responsif, setiap pemain dapat bermain dengan nyaman dan tenang di platform ini.
Promosi-Promosi dan Bonus Menarik
Ngamenjitu juga menawarkan bervariasi promosi dan bonus menarik bagi para pemain setia maupun yang baru bergabung. Dari bonus deposit hingga hadiah referral, setiap pemain memiliki kesempatan untuk meningkatkan kemenangan mereka dengan hadiah yang ditawarkan.
Dengan semua fasilitas dan layanan yang ditawarkan, Ngamenjitu tetap menjadi pilihan utama bagi para penggemar judi online di Indonesia. Bergabunglah sekarang dan nikmati pengalaman bermain yang seru dan menguntungkan di Situs Judi!
http://aviatormocambique.site/# como jogar aviator em mocambique
aviator jogo: aviator betano – aviator game
https://pinupcassino.pro/# pin-up
aviator game online: aviator – aviator login
khasiss.com
이때 그는 이미 현장을 통제하고 있었다.
smcasino7.com
장황후가 하렘의 영주라 이에 대해 아는 것이 없다?
aviator jogo: aviator game – aviator jogar
http://aviatoroyunu.pro/# aviator oyunu
Login Ngamenjitu
Portal Judi: Platform Togel Daring Terluas dan Terpercaya
Situs Judi telah menjadi salah satu portal judi online terbesar dan terpercaya di Indonesia. Dengan bervariasi pasaran yang disediakan dari Grup Semar, Ngamenjitu menawarkan sensasi main togel yang tak tertandingi kepada para penggemar judi daring.
Pasaran Terbaik dan Terlengkap
Dengan total 56 pasaran, Portal Judi menampilkan berbagai opsi terunggul dari market togel di seluruh dunia. Mulai dari pasaran klasik seperti Sydney, Singapore, dan Hongkong hingga pasaran eksotis seperti Thailand, Germany, dan Texas Day, setiap pemain dapat menemukan pasaran favorit mereka dengan mudah.
Langkah Main yang Praktis
Portal Judi menyediakan panduan cara main yang sederhana dipahami bagi para pemula maupun penggemar togel berpengalaman. Dari langkah-langkah pendaftaran hingga penarikan kemenangan, semua informasi tersedia dengan jelas di situs Portal Judi.
Ringkasan Terkini dan Informasi Terkini
Pemain dapat mengakses hasil terakhir dari setiap pasaran secara real-time di Portal Judi. Selain itu, info paling baru seperti jadwal bank online, gangguan, dan offline juga disediakan untuk memastikan kelancaran proses transaksi.
Berbagai Jenis Permainan
Selain togel, Portal Judi juga menawarkan berbagai jenis permainan kasino dan judi lainnya. Dari bingo hingga roulette, dari dragon tiger hingga baccarat, setiap pemain dapat menikmati berbagai pilihan permainan yang menarik dan menghibur.
Keamanan dan Kenyamanan Klien Dijamin
Ngamenjitu mengutamakan keamanan dan kenyamanan pelanggan. Dengan sistem security terbaru dan layanan pelanggan yang responsif, setiap pemain dapat bermain dengan nyaman dan tenang di platform ini.
Promosi-Promosi dan Hadiah Menarik
Situs Judi juga menawarkan bervariasi promosi dan bonus istimewa bagi para pemain setia maupun yang baru bergabung. Dari bonus deposit hingga bonus referral, setiap pemain memiliki kesempatan untuk meningkatkan kemenangan mereka dengan hadiah yang ditawarkan.
Dengan semua fitur dan layanan yang ditawarkan, Situs Judi tetap menjadi pilihan utama bagi para penggemar judi online di Indonesia. Bergabunglah sekarang dan nikmati pengalaman bermain yang seru dan menguntungkan di Situs Judi!
Hello.This post was extremely fascinating, particularly because I was searching for thoughts on this topic last Monday.
bistroduet.com
Fang Jifan은 더 이상 감히 죽지 않고 몸을 떨며 재빨리 세 번째 편지를 꺼냈습니다.
After all, what a great site and informative posts, I will upload inbound link – bookmark this web site? Regards, Reader.
обнал карт купить
Незаконные платформы, где предлагают обналичивание карт, составляют собой веб-ресурсы, специализирующиеся на рассмотрении и проведении неправомерных транзакций с финансовыми картами. На подобных платформах пользователи обмениваются данными, методами и опытом в области обналичивания, что влечет за собой противозаконные действия по получению к финансовым средствам.
Эти платформы могут предоставлять различные сервисы, связанные с преступной деятельностью, например фишинг, скимминг, вредное ПО и прочие методы для сбора данных с финансовых пластиковых карт. Кроме того обсуждаются темы, связанные с применением похищенных информации для совершения транзакций или вывода денег.
Пользователи незаконных платформ по обналичиванию карт могут оставаться анонимными и уходить от привлечения внимания органов безопасности. Участники могут обмениваться советами, предоставлять сервисы, связанные с обналичиванием, а также проводить сделки, направленные на финансовое преступление.
Необходимо отметить, что участие в подобных практиках не только представляет собой нарушение законов, но и может приводить к юридическим санкциям и наказанию.
обнал карт работа
Обналичивание карт – это незаконная деятельность, становящаяся все более распространенной в нашем современном мире электронных платежей. Этот вид мошенничества представляет тяжелые вызовы для банков, правоохранительных органов и общества в целом. В данной статье мы рассмотрим частоту встречаемости обналичивания карт, используемые методы и возможные последствия для жертв и общества.
Частота обналичивания карт:
Обналичивание карт является довольно распространенным явлением, и его частота постоянно растет с увеличением числа электронных транзакций. Киберпреступники применяют различные методы для получения доступа к финансовым средствам, включая фишинг, вредоносное программное обеспечение, скимминг и другие инновационные подходы.
Методы обналичивания карт:
Фишинг: Злоумышленники могут отправлять фальшивые электронные сообщения или создавать веб-сайты, имитирующие банковские системы, с целью получения личной информации от владельцев карт.
Скимминг: Злоумышленники устанавливают устройства скиммеры на банкоматах или терминалах для считывания данных с магнитных полос карт.
Вредоносное программное обеспечение: Киберпреступники разрабатывают вредоносные программы, которые заражают компьютеры и мобильные устройства, чтобы получить доступ к личным данным и банковским счетам.
Сетевые атаки: Атаки на системы банков и платежных платформ могут привести к утечке информации о картах и, следовательно, к их обналичиванию.
Последствия обналичивания карт:
Финансовые потери для клиентов: Владельцы карт могут столкнуться с денежными потерями, так как средства могут быть списаны с их счетов без их ведома.
Угроза безопасности данных: Обналичивание карт подчеркивает угрозу безопасности личных данных, что может привести к краже личной и финансовой информации.
Ущерб репутации банков: Банки и другие финансовые учреждения могут столкнуться с утратой доверия со стороны клиентов, если их системы безопасности оказываются уязвимыми.
Проблемы для экономики: Обналичивание карт создает экономический ущерб, поскольку оно стимулирует дополнительные затраты на борьбу с мошенничеством и восстановление утраченных средств.
Борьба с обналичиванием карт:
Совершенствование технологий безопасности: Банки и финансовые институты постоянно совершенствуют свои системы безопасности, чтобы предотвратить несанкционированный доступ к картам.
Образование и информирование: Обучение клиентов о методах мошенничества и том, как защитить свои данные, является важным шагом в борьбе с обналичиванием карт.
Сотрудничество с правоохранительными органами: Банки активно сотрудничают с правоохранительными органами для выявления и пресечения преступных схем.
Заключение:
Обналичивание карт – весомая угроза для финансовой стабильности и безопасности личных данных. Решение этой проблемы требует совместных усилий со стороны банков, правоохранительных органов и общества в целом. Только эффективная борьба с мошенничеством позволит обеспечить безопасность электронных платежей и защитить интересы всех участников финансовой системы.
I like the efforts you have put in this, regards for all the great posts.
jogar aviator online: aviator jogar – estrela bet aviator
aviator hilesi: aviator oyna slot – aviator bahis
kdslots
aviator bet: jogar aviator Brasil – pin up aviator
khasiss.com
“…” Zhang Yan은 앉지 않고 앉지 않고 몸을 구부 렸습니다.
aviator bet: aviator bet – jogar aviator online
can you buy zithromax over the counter in mexico: zithromax prescription – generic zithromax india
This is the right blog for anyone who wants to find out about this topic. You realize so much its almost hard to argue with you (not that I actually would want…HaHa). You definitely put a new spin on a topic thats been written about for years. Great stuff, just great!
indian pharmacies safe: reputable indian online pharmacy – indian pharmacy online indianpharm.store
top online pharmacy india Top online pharmacy in India buy medicines online in india indianpharm.store
Купить фальшивые рубли
Покупка поддельных купюр считается противозаконным и опасительным делом, которое способно закончиться тяжелым юридическими воздействиям либо постраданию индивидуальной финансовой благосостояния. Вот некоторые примет, по какой причине закупка лживых купюр представляет собой рискованной и недопустимой:
Нарушение законов:
Приобретение либо эксплуатация контрафактных денег являются преступлением, подрывающим нормы территории. Вас в состоянии поддать уголовной ответственности, которое может повлечь за собой аресту, штрафам иначе тюремному заключению.
Ущерб доверию:
Контрафактные купюры подрывают уверенность к денежной механизму. Их обращение порождает возможность для порядочных людей и бизнесов, которые могут попасть в неожиданными расходами.
Экономический ущерб:
Разведение лживых денег осуществляет воздействие на хозяйство, вызывая распределение денег и ухудшающая глобальную финансовую стабильность. Это может привести к потере доверия к денежной единице.
Риск обмана:
Люди, какие, вовлечены в изготовлением лживых банкнот, не обязаны поддерживать какие-либо параметры степени. Фальшивые деньги могут стать легко распознаваемы, что, в итоге повлечь за собой потерям для тех, кто попытается их использовать.
Юридические последствия:
В ситуации захвата при применении контрафактных денег, вас имеют возможность наказать штрафом, и вы столкнетесь с юридическими трудностями. Это может повлиять на вашем будущем, включая проблемы с трудоустройством и кредитной историей.
Благосостояние общества и личное благополучие зависят от честности и доверии в денежной области. Приобретение лживых денег противоречит этим принципам и может порождать серьезные последствия. Советуем соблюдать норм и заниматься исключительно правомерными финансовыми операциями.
crazy-slot1.com
장교는 자신의 차례가 되면 원하는 병사를 훈련시켜야 하기 때문에…
магазин фальшивых денег купить
Покупка поддельных банкнот приравнивается к недозволенным и потенциально опасным поступком, что в состоянии повлечь за собой глубоким законным наказаниям либо постраданию своей финансовой надежности. Вот несколько других причин, из-за чего приобретение поддельных банкнот является опасительной и неуместной:
Нарушение законов:
Закупка либо использование контрафактных банкнот приравниваются к преступлением, противоречащим правила страны. Вас могут поддать уголовной ответственности, которое может повлечь за собой тюремному заключению, денежным наказаниям или постановлению под стражу.
Ущерб доверию:
Лживые деньги ослабляют доверенность в финансовой организации. Их обращение создает опасность для благоприятных граждан и бизнесов, которые могут столкнуться с непредвиденными расходами.
Экономический ущерб:
Разведение фальшивых банкнот оказывает воздействие на хозяйство, приводя к инфляцию что ухудшает всеобщую экономическую стабильность. Это может закончиться утрате уважения к денежной единице.
Риск обмана:
Те, которые, занимается производством фальшивых банкнот, не обязаны поддерживать какие угодно параметры качества. Фальшивые деньги могут выйти легко выявлены, что в итоге закончится потерям для тех пытается использовать их.
Юридические последствия:
При случае лишения свободы за использование лживых банкнот, вас имеют возможность наказать штрафом, и вы столкнетесь с юридическими проблемами. Это может отразиться на вашем будущем, в том числе трудности с трудоустройством и кредитной историей.
Общественное и личное благополучие зависят от честности и доверии в финансовых отношениях. Покупка поддельных денег нарушает эти принципы и может представлять серьезные последствия. Рекомендуется соблюдать норм и вести только законными финансовыми сделками.
https://canadianpharmlk.com/# canadian world pharmacy canadianpharm.store
pchelografiya.com
그러나 그의 아들이 그에게 이 질문을 했을 때 그는 어안이 벙벙했습니다.
https://indianpharm24.shop/# best india pharmacy indianpharm.store
http://indianpharm24.shop/# online pharmacy india indianpharm.store
http://mexicanpharm24.shop/# reputable mexican pharmacies online mexicanpharm.shop
online shopping pharmacy india: Best Indian pharmacy – top 10 online pharmacy in india indianpharm.store
Good post and straight to the point. I don’t know if this is truly the best place to ask but do you folks have any thoughts on where to get some professional writers? Thanks in advance 🙂
http://mexicanpharm24.shop/# pharmacies in mexico that ship to usa mexicanpharm.shop
https://canadianpharmlk.com/# canadapharmacyonline legit canadianpharm.store
mexico pharmacies prescription drugs mexico drug stores pharmacies mexican online pharmacies prescription drugs mexicanpharm.shop
http://indianpharm24.shop/# online pharmacy india indianpharm.store
amoxicillin 500 mg where to buy: amoxicillin dosage for adults – amoxicillin azithromycin
https://amoxilst.pro/# generic amoxicillin 500mg
mega-slot66.com
비록…그건 도박일 뿐인데, 요점이 뭐야?
http://clomidst.pro/# can i order generic clomid price
khasiss.com
“삼촌을 설명하십시오.”Fang Jifan은 그를 때리기 위해 주먹을 들어 올렸습니다.
where buy cheap clomid without dr prescription can i order cheap clomid without rx where can i get cheap clomid pills
5 prednisone in mexico: п»їprednisone 10 mg tablet – prednisone 1 mg daily
amoxicillin 500 mg tablet: amoxicillin order online – where can i buy amoxicillin without prec
купить фальшивые рубли
Осознание сущности и угроз связанных с обналом кредитных карт может помочь людям предупреждать атак и защищать свои финансовые ресурсы. Обнал (отмывание) кредитных карт — это механизм использования украденных или нелегально добытых кредитных карт для осуществления финансовых транзакций с целью скрыть их происхождения и заблокировать отслеживание.
Вот некоторые способов, которые могут содействовать в уклонении от обнала кредитных карт:
Сохранение личной информации: Будьте осторожными в отношении предоставления личной информации, особенно онлайн. Избегайте предоставления картовых номеров, кодов безопасности и дополнительных конфиденциальных данных на сомнительных сайтах.
Сильные пароли: Используйте безопасные и уникальные пароли для своих банковских аккаунтов и кредитных карт. Регулярно изменяйте пароли.
Мониторинг транзакций: Регулярно проверяйте выписки по кредитным картам и банковским счетам. Это способствует своевременному выявлению подозрительных транзакций.
Защита от вирусов: Используйте антивирусное программное обеспечение и вносите обновления его регулярно. Это поможет защитить от вредоносные программы, которые могут быть использованы для похищения данных.
Осмотрительное поведение в социальных медиа: Будьте осторожными в сетевых платформах, избегайте опубликования чувствительной информации, которая может быть использована для взлома вашего аккаунта.
Уведомление банка: Если вы заметили какие-либо подозрительные операции или утерю карты, сразу свяжитесь с вашим банком для отключения карты.
Получение знаний: Будьте внимательными к новым методам мошенничества и обучайтесь тому, как противостоять их.
Избегая легковерия и принимая меры предосторожности, вы можете уменьшить риск стать жертвой обнала кредитных карт.
http://clomidst.pro/# clomid order
https://clomidst.pro/# how can i get clomid tablets
Very interesting topic, appreciate it for putting up. “Time flies like an arrow. Fruit flies like a banana.” by Lisa Grossman.
https://prednisonest.pro/# buy prednisone with paypal canada
how can i get cheap clomid for sale cost of cheap clomid can i order generic clomid pills
can i buy clomid without a prescription: get generic clomid price – buy generic clomid without rx
amoxicillin online without prescription: amoxicillin side effects – ampicillin amoxicillin
http://amoxilst.pro/# cost of amoxicillin 875 mg
manga online
buying prescription drugs from canada Best online pharmacy online pharmacy no prescription needed
https://edpills.guru/# online erectile dysfunction pills
cheapest pharmacy prescription drugs: pharmacy online – online pharmacy without prescription
mersingtourism.com
그에게 돈은…그 밖에 있는 것일 뿐, 벌면 벌수록 더 뜨거워진다.
ttbslot.com
Ma Wensheng은 미소를 지으며 수염을 쓰다듬으며 “충실하고 의롭고 해와 달과 함께 영광을 얻으십시오! “라고 말했습니다.
http://edpills.guru/# п»їed pills online
online medication without prescription canadian prescription prices prescription drugs online canada
https://onlinepharmacy.cheap/# pharmacy coupons
best no prescription online pharmacy: no prescription needed pharmacy – no prescription needed pharmacy
ttbslot.com
하지만 이때 Fang Jifan은 미소를 지으며 Zhu Houzhao를 바라 보았습니다.
https://pharmnoprescription.pro/# mexican pharmacy no prescription
online pharmacies without prescriptions: online pharmacy reviews no prescription – no prescription pharmacy
hoki1881
http://pharmnoprescription.pro/# online pharmacy without a prescription
low cost ed meds: cheap ed treatment – ed doctor online
cheapest ed pills cheapest ed medication cheap ed meds
non prescription online pharmacy india no prescription drugs online buy prescription drugs online without
https://canadianpharm.guru/# canadian pharmacy 24h com safe
world pharmacy india: Online medicine home delivery – india online pharmacy
https://indianpharm.shop/# indian pharmacy paypal
https://canadianpharm.guru/# escrow pharmacy canada
I love it when people come together and share opinions, great blog, keep it up.
http://pharmacynoprescription.pro/# no prescription needed online pharmacy
https://mexicanpharm.online/# purple pharmacy mexico price list
qiyezp.com
하지만 누가 생각이나 했을까요… 대신 누군가에게 놀아나는 것 같았습니다.
When I initially commented I clicked the “Notify me when new comments are added” checkbox and now each time a comment is added I get three e-mails with the same comment. Is there any way you can remove me from that service? Thanks!
I like this internet site because so much utile stuff on here : D.
http://mexicanpharm.online/# medication from mexico pharmacy
https://pharmacynoprescription.pro/# meds no prescription
qiyezp.com
이 소식을 들은 순천주 장라이(張來)가 행정관, 재판관들과 함께 그를 맞이하러 왔다.
http://mexicanpharm.online/# mexican online pharmacies prescription drugs
https://pharmacynoprescription.pro/# online drugs without prescription
http://pharmacynoprescription.pro/# no prescription medicine
https://pharmacynoprescription.pro/# buy medication online with prescription
https://canadianpharm.guru/# canadian pharmacy review
buying prescription drugs in mexico online mexico drug stores pharmacies purple pharmacy mexico price list
http://canadianpharm.guru/# canadian pharmacy mall
sandyterrace.com
이 말을 들은 두 쥬렌은 갑자기… 머리가 터졌다.
http://mexicanpharm.online/# mexican mail order pharmacies
http://indianpharm.shop/# buy prescription drugs from india
purple pharmacy mexico price list mexico pharmacies prescription drugs mexico pharmacies prescription drugs
http://pharmacynoprescription.pro/# medications online without prescriptions
Тор веб-навигатор – это особый браузер, который предназначен для обеспечения анонимности и надежности в Сети. Он разработан на инфраструктуре Тор (The Onion Router), позволяющая участникам пересылать данными по дистрибутированную сеть серверов, что делает сложным отслеживание их поступков и установление их локации.
Главная характеристика Тор браузера состоит в его умении маршрутизировать интернет-трафик через несколько узлов сети Тор, каждый из которых шифрует информацию перед передачей последующему узлу. Это обеспечивает многочисленное количество слоев (поэтому и титул “луковая маршрутизация” – “The Onion Router”), что создает почти невозможным прослушивание и установление пользователей.
Тор браузер периодически применяется для пересечения цензуры в государствах, где ограничивается доступ к конкретным веб-сайтам и сервисам. Он также даёт возможность пользователям обеспечивать приватность своих онлайн-действий, наподобие просмотр веб-сайтов, коммуникация в чатах и отправка электронной почты, избегая отслеживания и мониторинга со стороны интернет-провайдеров, государственных агентств и киберпреступников.
Однако рекомендуется помнить, что Тор браузер не обеспечивает полной анонимности и устойчивости, и его применение может быть ассоциировано с опасностью доступа к противозаконным контенту или деятельности. Также может быть замедление скорости интернет-соединения из-за
hoki 1881
hoki 1881
etsyweddingteam.com
素晴らしい記事!共有せずにはいられません。
https://canadianpharm.guru/# canadian pharmacy no scripts
http://canadianpharm.guru/# canadian pharmacy review
canada drug pharmacy: canadian pharmacy online store – canadian drug
canadian pharmacy prescription online pharmacy without prescriptions no prescription online pharmacy
qiyezp.com
Xiao Jing은 똑똑한 사람으로 Hongzhi 황제에게 미소를 지으며 모든 문장에 대해 생각했습니다.
pin-up casino indir: pin up giris – pin up casino guncel giris
https://slotsiteleri.guru/# slot siteleri
http://slotsiteleri.guru/# yasal slot siteleri
http://slotsiteleri.guru/# deneme bonusu veren siteler
bonus veren casino slot siteleri: en yeni slot siteleri – canl? slot siteleri
animehangover.com
이거… 국고의 현재 수입을 또 넘지 않을까요?
aviator oyna 100 tl: ucak oyunu bahis aviator – aviator oyna 100 tl
https://gatesofolympus.auction/# pragmatic play gates of olympus
даркнет запрещён
Покупки в Даркнете: Иллюзии и Факты
Темный интернет, загадочная область сети, привлекает внимание участников своей анонимностью и возможностью возможностью купить самые разнообразные продукты и сервисы без лишних вопросов. Однако, переход в этот мир темных рынков сопряжено с комплексом рисков и сложностей, о которых необходимо понимать перед совершением покупок.
Что такое скрытая часть веба и как это функционирует?
Для тех, кому не знакомо с этим термином, скрытая часть веба – это сегмент интернета, скрытая от обычных поисковых систем. В скрытой части веба имеются специальные торговые площадки, где можно найти почти все, что угодно : от запрещённых веществ и боеприпасов до взломанных аккаунтов и фальшивых документов.
Иллюзии о покупках в темном интернете
Тайность защищена: При всём том, использование технологий анонимности, например Tor, может помочь скрыть от глаз вашу активность в интернете, тайность в подпольной сети не является абсолютной. Существует опасность, что вашу личные данные могут выявить обманщики или даже сотрудники правоохранительных органов.
Все товары – качественные товары: В Даркнете можно обнаружить много поставщиков, продающих продукцию и услуги. Однако, нельзя гарантировать качественность или подлинность товара, поскольку нет возможности провести проверку до заказа.
Легальные сделки без последствий: Многие пользователи неправильно думают, что заказывая товары в скрытой части веба, они подвергают себя риску низкому риску, чем в реальной жизни. Однако, заказывая противоправные вещи или сервисы, вы рискуете уголовной ответственности.
Реальность покупок в скрытой части веба
Опасности обмана и афер: В темном интернете много мошенников, готовы к обману недостаточно осторожных пользователей. Они могут предложить фальшивые товары или просто исчезнуть с вашими деньгами.
Опасность легальных органов: Пользователи Даркнета подвергают себя риску к уголовной ответственности за приобретение и заказ неправомерных продуктов и услуг.
Непредсказуемость результатов: Не каждая сделка в темном интернете приводят к успешному результату. Качество вещей может оказаться низким, а сам процесс приобретения может привести к неприятным последствиям.
Советы для безопасных сделок в подпольной сети
Проводите тщательное исследование продавца и товара перед осуществлением заказа.
Используйте безопасные программы и сервисы для обеспечения вашей анонимности и безопасности.
Платите только безопасными методами, например, криптовалютами, и не раскрывайте личные данные.
Будьте предельно внимательны и осторожны во всех совершаемых действиях и выбранных вариантах.
Заключение
Транзакции в скрытой части веба могут быть как захватывающим, так и опасным опытом. Понимание возможных опасностей и принятие необходимых мер предосторожности помогут уменьшить риск негативных последствий и обеспечить безопасность при покупках в этом неизведанном мире интернета.
sweet bonanza bahis: sweet bonanza nas?l oynan?r – sweet bonanza bahis
gates of olympus nas?l para kazanilir: gates of olympus oyna ucretsiz – gate of olympus hile
aviator oyna: aviator ucak oyunu – aviator sinyal hilesi
aviator hilesi ucretsiz: aviator hilesi – ucak oyunu bahis aviator
https://aviatoroyna.bid/# aviator hile
sweet bonanza 100 tl: sweet bonanza siteleri – sweet bonanza giris
gates of olympus max win: gates of olympus demo turkce oyna – gates of olympus s?rlar?
http://aviatoroyna.bid/# aviator sinyal hilesi ucretsiz
https://gatesofolympus.auction/# gates of olympus demo free spin
gates of olympus hilesi: gates of olympus demo turkce – gates of olympus 1000 demo
http://aviatoroyna.bid/# aviator sinyal hilesi ücretsiz
http://indianpharmacy.icu/# top online pharmacy india
buy medicines online in india: Cheapest online pharmacy – indian pharmacy online
otraresacamas.com
知識が豊富で読みやすい素晴らしい記事でした。
п»їlegitimate online pharmacies india: indian pharmacy – Online medicine order
https://mexicanpharmacy.shop/# buying prescription drugs in mexico
canadian pharmacies compare: trustworthy canadian pharmacy – canadian pharmacy price checker
cheap canadian pharmacy online: Prescription Drugs from Canada – best canadian online pharmacy
сеть даркнет
Подпольная часть сети: запрещённое пространство виртуальной сети
Теневой уровень интернета, скрытый уголок интернета продолжает вызывать интерес внимание и сообщества, а также служб безопасности. Этот скрытый уровень сети известен своей непрозрачностью и возможностью проведения противоправных действий под тенью анонимности.
Основа теневого уровня интернета состоит в том, что он не доступен для популярных браузеров. Для доступа к этому уровню необходимы специальные инструменты и программы, обеспечивающие скрытность пользователей. Это вызывает прекрасные условия для различных незаконных действий, включая сбыт наркотиков, продажу оружия, кражу личных данных и другие противоправные действия.
В свете растущую угрозу, многие страны приняли законодательные инициативы, направленные на ограничение доступа к теневому уровню интернета и преследование лиц совершающих противозаконные действия в этом скрытом мире. Однако, несмотря на принятые меры, борьба с теневым уровнем интернета представляет собой сложную задачу.
Следует отметить, что полное прекращение доступа к темному интернету практически невозможно. Даже при принятии строгих контрмер, возможность доступа к данному уровню сети все еще осуществим через различные технологии и инструменты, применяемые для обхода ограничений.
В дополнение к законодательным инициативам, имеются также проекты сотрудничества между правоохранительными органами и технологическими компаниями для противодействия незаконным действиям в подпольной части сети. Тем не менее, эта борьба требует не только технических решений, но и улучшения методов обнаружения и пресечения незаконных действий в этой среде.
В итоге, несмотря на введенные запреты и предпринятые усилия в борьбе с преступностью, темный интернет остается серьезной проблемой, требующей комплексного подхода и совместных усилий как со стороны правоохранительных органов, а также технологических организаций.
reputable indian online pharmacy: reputable indian online pharmacy – india online pharmacy
http://mexicanpharmacy.shop/# pharmacies in mexico that ship to usa
top online pharmacy india: Cheapest online pharmacy – online pharmacy india
https://zithromaxall.com/# zithromax 500 mg lowest price online
buy amoxicillin 250mg amoxacillian without a percription where to buy amoxicillin
prednisone 40 mg: prednisone without a prescription – prednisone 20 mg tablet price
https://prednisoneall.com/# over the counter prednisone pills
qiyezp.com
과거 점쟁이들은 호랑이가 부지런하다고 했습니다.
average cost of prednisone cheapest prednisone no prescription canadian online pharmacy prednisone
prednisone pill: prednisone 5 50mg tablet price – generic prednisone online
https://sildenafiliq.com/# Sildenafil Citrate Tablets 100mg
Kamagra 100mg: Kamagra 100mg price – Kamagra 100mg
Tadalafil price: Tadalafil Tablet – Tadalafil price
Buy Tadalafil 10mg: Generic Tadalafil 20mg price – Generic Cialis price
http://kamagraiq.com/# buy kamagra online usa
onair2tv.com
하지만…이 사람들은…왜…감히…
https://tadalafiliq.com/# Cialis 20mg price
Buy Cialis online cialis without a doctor prescription Cialis 20mg price
https://tadalafiliq.com/# cialis for sale
usareallservice.com
このブログは本当に役立つ情報が満載で、大好きです。
https://tadalafiliq.shop/# Cialis over the counter
Cialis over the counter: tadalafil iq – Tadalafil price
https://kamagraiq.shop/# Kamagra 100mg price
https://tadalafiliq.shop/# Tadalafil Tablet
https://kamagraiq.shop/# Kamagra Oral Jelly
Kamagra 100mg price: kamagra best price – Kamagra 100mg
generic sildenafil buy viagra online Viagra without a doctor prescription Canada
https://sildenafiliq.com/# Cheapest Sildenafil online
sandyterrace.com
사실은 조금 부끄럽습니다. 그는 실제로 짧은 거리 만 걸었다는 것을 알았습니다.
Kamagra 100mg price: kamagra best price – п»їkamagra
nikontinoll.com
하지만… 이 표준은 모든 왕조의 황제들이 항상 믿었던 것입니다.
indian pharmacy online: indian pharmacy – online shopping pharmacy india
http://indianpharmgrx.com/# buy medicines online in india
kantor bola
KANTORBOLA situs gamin online terbaik 2024 yang menyediakan beragam permainan judi online easy to win , mulai dari permainan slot online , taruhan judi bola , taruhan live casino , dan toto macau . Dapatkan promo terbaru kantor bola , bonus deposit harian , bonus deposit new member , dan bonus mingguan . Kunjungi link kantorbola untuk melakukan pendaftaran .
indian pharmacy online: reputable indian pharmacies – indianpharmacy com
canadian neighbor pharmacy: Canada pharmacy – canadian mail order pharmacy
kantor bola
Informasi RTP Live Hari Ini Dari Situs RTPKANTORBOLA
Situs RTPKANTORBOLA merupakan salah satu situs yang menyediakan informasi lengkap mengenai RTP (Return to Player) live hari ini. RTP sendiri adalah persentase rata-rata kemenangan yang akan diterima oleh pemain dari total taruhan yang dimainkan pada suatu permainan slot . Dengan adanya informasi RTP live, para pemain dapat mengukur peluang mereka untuk memenangkan suatu permainan dan membuat keputusan yang lebih cerdas saat bermain.
Situs RTPKANTORBOLA menyediakan informasi RTP live dari berbagai permainan provider slot terkemuka seperti Pragmatic Play , PG Soft , Habanero , IDN Slot , No Limit City dan masih banyak rtp permainan slot yang bisa kami cek di situs RTP Kantorboal . Dengan menyediakan informasi yang akurat dan terpercaya, situs ini menjadi sumber informasi yang penting bagi para pemain judi slot online di Indonesia .
Salah satu keunggulan dari situs RTPKANTORBOLA adalah penyajian informasi yang terupdate secara real-time. Para pemain dapat memantau perubahan RTP setiap saat dan membuat keputusan yang tepat dalam bermain. Selain itu, situs ini juga menyediakan informasi mengenai RTP dari berbagai provider permainan, sehingga para pemain dapat membandingkan dan memilih permainan dengan RTP tertinggi.
Informasi RTP live yang disediakan oleh situs RTPKANTORBOLA juga sangat lengkap dan mendetail. Para pemain dapat melihat RTP dari setiap permainan, baik itu dari aspek permainan itu sendiri maupun dari provider yang menyediakannya. Hal ini sangat membantu para pemain dalam memilih permainan yang sesuai dengan preferensi dan gaya bermain mereka.
Selain itu, situs ini juga menyediakan informasi mengenai RTP live dari berbagai provider judi slot online terpercaya. Dengan begitu, para pemain dapat memilih permainan slot yang memberikan RTP terbaik dan lebih aman dalam bermain. Informasi ini juga membantu para pemain untuk menghindari potensi kerugian dengan bermain pada game slot online dengan RTP rendah .
Situs RTPKANTORBOLA juga memberikan pola dan ulasan mengenai permainan-permainan dengan RTP tertinggi. Para pemain dapat mempelajari strategi dan tips dari para ahli untuk meningkatkan peluang dalam memenangkan permainan. Analisis dan ulasan ini disajikan secara jelas dan mudah dipahami, sehingga dapat diaplikasikan dengan baik oleh para pemain.
Informasi RTP live yang disediakan oleh situs RTPKANTORBOLA juga dapat membantu para pemain dalam mengelola keuangan mereka. Dengan mengetahui RTP dari masing-masing permainan slot , para pemain dapat mengatur taruhan mereka dengan lebih bijak. Hal ini dapat membantu para pemain untuk mengurangi risiko kerugian dan meningkatkan peluang untuk mendapatkan kemenangan yang lebih besar.
Untuk mengakses informasi RTP live dari situs RTPKANTORBOLA, para pemain tidak perlu mendaftar atau membayar biaya apapun. Situs ini dapat diakses secara gratis dan tersedia untuk semua pemain judi online. Dengan begitu, semua orang dapat memanfaatkan informasi yang disediakan oleh situs RTP Kantorbola untuk meningkatkan pengalaman dan peluang mereka dalam bermain judi online.
Demikianlah informasi mengenai RTP live hari ini dari situs RTPKANTORBOLA. Dengan menyediakan informasi yang akurat, terpercaya, dan lengkap, situs ini menjadi sumber informasi yang penting bagi para pemain judi online. Dengan memanfaatkan informasi yang disediakan, para pemain dapat membuat keputusan yang lebih cerdas dan meningkatkan peluang mereka untuk memenangkan permainan. Selamat bermain dan semoga sukses!
sandyterrace.com
Fang Jifan이 나간 후 Xishan Jianye가 가장 먼저 조사했습니다.
india pharmacy: indian pharmacy delivery – pharmacy website india
Mengenal Situs Gaming Online Terbaik Kantorbola
Kantorbola merupakan situs gaming online terbaik yang menawarkan pengalaman bermain yang seru dan mengasyikkan bagi para pecinta game. Dengan berbagai pilihan game menarik dan grafis yang memukau, Kantorbola menjadi pilihan utama bagi para gamers yang ingin mencari hiburan dan tantangan baru. Dengan layanan customer service yang ramah dan profesional, serta sistem keamanan yang terjamin, Kantorbola siap memberikan pengalaman bermain yang terbaik dan menyenangkan bagi semua membernya. Jadi, tunggu apalagi? Bergabunglah sekarang dan rasakan sensasi seru bermain game di Kantorbola!
Situs kantor bola menyediakan beberapa link alternatif terbaru
Situs kantor bola merupakan salah satu situs gaming online terbaik yang menyediakan berbagai link alternatif terbaru untuk memudahkan para pengguna dalam mengakses situs tersebut. Dengan adanya link alternatif terbaru ini, para pengguna dapat tetap mengakses situs kantor bola meskipun terjadi pemblokiran dari pemerintah atau internet positif. Hal ini tentu menjadi kabar baik bagi para pecinta judi online yang ingin tetap bermain tanpa kendala akses ke situs kantor bola.
Dengan menyediakan beberapa link alternatif terbaru, situs kantor bola juga dapat memberikan variasi akses kepada para pengguna. Hal ini memungkinkan para pengguna untuk memilih link alternatif mana yang paling cepat dan stabil dalam mengakses situs tersebut. Dengan demikian, pengalaman bermain judi online di situs kantor bola akan menjadi lebih lancar dan menyenangkan.
Selain itu, situs kantor bola juga menunjukkan komitmennya dalam memberikan pelayanan terbaik kepada para pengguna dengan menyediakan link alternatif terbaru secara berkala. Dengan begitu, para pengguna tidak perlu khawatir akan kehilangan akses ke situs kantor bola karena selalu ada link alternatif terbaru yang dapat digunakan sebagai backup. Keberadaan link alternatif tersebut juga menunjukkan bahwa situs kantor bola selalu berusaha untuk tetap eksis dan dapat diakses oleh para pengguna setianya.
Secara keseluruhan, kehadiran beberapa link alternatif terbaru dari situs kantor bola merupakan salah satu bentuk komitmen dari situs tersebut dalam memberikan kemudahan dan kenyamanan kepada para pengguna. Dengan adanya link alternatif tersebut, para pengguna dapat terus mengakses situs kantor bola tanpa hambatan apapun. Hal ini tentu akan semakin meningkatkan popularitas situs kantor bola sebagai salah satu situs gaming online terbaik di Indonesia. Berikut beberapa link alternatif dari situs kantorbola , diantaranya .
1. Link Kantorbola77
Link Kantorbola77 merupakan salah satu situs gaming online terbaik yang saat ini banyak diminati oleh para pecinta judi online. Dengan berbagai pilihan permainan yang lengkap dan berkualitas, situs ini mampu memberikan pengalaman bermain yang memuaskan bagi para membernya. Selain itu, Kantorbola77 juga menawarkan berbagai bonus dan promo menarik yang dapat meningkatkan peluang kemenangan para pemain.
Salah satu keunggulan dari Link Kantorbola77 adalah sistem keamanan yang sangat terjamin. Dengan teknologi enkripsi yang canggih, situs ini menjaga data pribadi dan transaksi keuangan para membernya dengan sangat baik. Hal ini membuat para pemain merasa aman dan nyaman saat bermain di Kantorbola77 tanpa perlu khawatir akan adanya kebocoran data atau tindakan kecurangan yang merugikan.
Selain itu, Link Kantorbola77 juga menyediakan layanan pelanggan yang siap membantu para pemain 24 jam non-stop. Tim customer service yang profesional dan responsif siap membantu para member dalam menyelesaikan berbagai kendala atau pertanyaan yang mereka hadapi saat bermain. Dengan layanan yang ramah dan efisien, Kantorbola77 menempatkan kepuasan para pemain sebagai prioritas utama mereka.
Dengan reputasi yang baik dan pengalaman yang telah teruji, Link Kantorbola77 layak untuk menjadi pilihan utama bagi para pecinta judi online. Dengan berbagai keunggulan yang dimilikinya, situs ini memberikan pengalaman bermain yang memuaskan dan menguntungkan bagi para membernya. Jadi, jangan ragu untuk bergabung dan mencoba keberuntungan Anda di Kantorbola77.
2. Link Kantorbola88
Link kantorbola88 adalah salah satu situs gaming online terbaik yang harus dikenal oleh para pecinta judi online. Dengan menyediakan berbagai jenis permainan seperti judi bola, casino, slot online, poker, dan banyak lagi, kantorbola88 menjadi pilihan utama bagi para pemain yang ingin mencoba keberuntungan mereka. Link ini memberikan akses mudah dan cepat untuk para pemain yang ingin bermain tanpa harus repot mencari situs judi online yang terpercaya.
Selain itu, kantorbola88 juga dikenal sebagai situs yang memiliki reputasi baik dalam hal pelayanan dan keamanan. Dengan sistem keamanan yang canggih dan profesional, para pemain dapat bermain tanpa perlu khawatir akan kebocoran data pribadi atau transaksi keuangan mereka. Selain itu, layanan pelanggan yang ramah dan responsif juga membuat pengalaman bermain di kantorbola88 menjadi lebih menyenangkan dan nyaman.
Selain itu, link kantorbola88 juga menawarkan berbagai bonus dan promosi menarik yang dapat dinikmati oleh para pemain. Mulai dari bonus deposit, cashback, hingga bonus referral, semua memberikan kesempatan bagi pemain untuk mendapatkan keuntungan lebih saat bermain di situs ini. Dengan adanya bonus-bonus tersebut, kantorbola88 terus berusaha memberikan yang terbaik bagi para pemainnya agar selalu merasa puas dan senang bermain di situs ini.
Dengan reputasi yang baik, pelayanan yang prima, keamanan yang terjamin, dan bonus yang menggiurkan, link kantorbola88 adalah pilihan yang tepat bagi para pemain judi online yang ingin merasakan pengalaman bermain yang seru dan menguntungkan. Dengan bergabung di situs ini, para pemain dapat merasakan sensasi bermain judi online yang berkualitas dan terpercaya, serta memiliki peluang untuk mendapatkan keuntungan besar. Jadi, jangan ragu untuk mencoba keberuntungan Anda di kantorbola88 dan nikmati pengalaman bermain yang tak terlupakan.
3. Link Kantorbola88
Kantorbola99 merupakan salah satu situs gaming online terbaik yang dapat menjadi pilihan bagi para pecinta judi online. Situs ini menawarkan berbagai permainan menarik seperti judi bola, casino online, slot online, poker, dan masih banyak lagi. Dengan berbagai pilihan permainan yang disediakan, para pemain dapat menikmati pengalaman berjudi yang seru dan mengasyikkan.
Salah satu keunggulan dari Kantorbola99 adalah sistem keamanan yang sangat terjamin. Situs ini menggunakan teknologi enkripsi terbaru untuk melindungi data pribadi dan transaksi keuangan para pemain. Dengan demikian, para pemain bisa bermain dengan tenang tanpa perlu khawatir tentang kebocoran data pribadi atau kecurangan dalam permainan.
Selain itu, Kantorbola99 juga menawarkan berbagai bonus dan promo menarik bagi para pemain setianya. Mulai dari bonus deposit, bonus cashback, hingga bonus referral yang dapat meningkatkan peluang para pemain untuk meraih kemenangan. Dengan adanya bonus dan promo ini, para pemain dapat merasa lebih diuntungkan dan semakin termotivasi untuk bermain di situs ini.
Dengan reputasi yang baik dan pengalaman yang telah terbukti, Kantorbola99 menjadi pilihan yang tepat bagi para pecinta judi online. Dengan pelayanan yang ramah dan responsif, para pemain juga dapat mendapatkan bantuan dan dukungan kapan pun dibutuhkan. Jadi, tidak heran jika Kantorbola99 menjadi salah satu situs gaming online terbaik yang banyak direkomendasikan oleh para pemain judi online.
Promo Terbaik Dari Situs kantorbola
Kantorbola merupakan salah satu situs gaming online terbaik yang menyediakan berbagai jenis permainan menarik seperti judi bola, casino, poker, slots, dan masih banyak lagi. Situs ini telah menjadi pilihan utama bagi para pecinta judi online karena reputasinya yang terpercaya dan kualitas layanannya yang prima. Selain itu, Kantorbola juga seringkali memberikan promo-promo menarik kepada para membernya, salah satunya adalah promo terbaik yang dapat meningkatkan peluang kemenangan para pemain.
Promo terbaik dari situs Kantorbola biasanya berupa bonus deposit, cashback, maupun event-event menarik yang diadakan secara berkala. Dengan adanya promo-promo ini, para pemain memiliki kesempatan untuk mendapatkan keuntungan lebih besar dan juga kesempatan untuk memenangkan hadiah-hadiah menarik. Selain itu, promo-promo ini juga menjadi daya tarik bagi para pemain baru yang ingin mencoba bermain di situs Kantorbola.
Salah satu promo terbaik dari situs Kantorbola yang paling diminati adalah bonus deposit new member sebesar 100%. Dengan bonus ini, para pemain baru bisa mendapatkan tambahan saldo sebesar 100% dari jumlah deposit yang mereka lakukan. Hal ini tentu saja menjadi kesempatan emas bagi para pemain untuk bisa bermain lebih lama dan meningkatkan peluang kemenangan mereka. Selain itu, Kantorbola juga selalu memberikan promo-promo menarik lainnya yang dapat dinikmati oleh semua membernya.
Dengan berbagai promo terbaik yang ditawarkan oleh situs Kantorbola, para pemain memiliki banyak kesempatan untuk meraih kemenangan besar dan mendapatkan pengalaman bermain judi online yang lebih menyenangkan. Jadi, jangan ragu untuk bergabung dan mencoba keberuntungan Anda di situs gaming online terbaik ini. Dapatkan promo-promo menarik dan nikmati berbagai jenis permainan seru hanya di Kantorbola.
Deposit Kilat Di Kantorbola Melalui QRIS
Deposit kilat di Kantorbola melalui QRIS merupakan salah satu fitur yang mempermudah para pemain judi online untuk melakukan transaksi secara cepat dan aman. Dengan menggunakan QRIS, para pemain dapat melakukan deposit dengan mudah tanpa perlu repot mencari nomor rekening atau melakukan transfer manual.
QRIS sendiri merupakan sistem pembayaran digital yang memanfaatkan kode QR untuk memfasilitasi transaksi pembayaran. Dengan menggunakan QRIS, para pemain judi online dapat melakukan deposit hanya dengan melakukan pemindaian kode QR yang tersedia di situs Kantorbola. Proses deposit pun dapat dilakukan dalam waktu yang sangat singkat, sehingga para pemain tidak perlu menunggu lama untuk bisa mulai bermain.
Keunggulan deposit kilat di Kantorbola melalui QRIS adalah kemudahan dan kecepatan transaksi yang ditawarkan. Para pemain judi online tidak perlu lagi repot mencari nomor rekening atau melakukan transfer manual yang memakan waktu. Cukup dengan melakukan pemindaian kode QR, deposit dapat langsung terproses dan saldo akun pemain pun akan langsung bertambah.
Dengan adanya fitur deposit kilat di Kantorbola melalui QRIS, para pemain judi online dapat lebih fokus pada permainan tanpa harus terganggu dengan urusan transaksi. QRIS memungkinkan para pemain untuk melakukan deposit kapan pun dan di mana pun dengan mudah, sehingga pengalaman bermain judi online di Kantorbola menjadi lebih menyenangkan dan praktis.
Dari ulasan mengenai mengenal situs gaming online terbaik Kantorbola, dapat disimpulkan bahwa situs tersebut menawarkan berbagai jenis permainan yang menarik dan populer di kalangan para penggemar game. Dengan tampilan yang menarik dan user-friendly, Kantorbola memberikan pengalaman bermain yang menyenangkan dan memuaskan bagi para pemain. Selain itu, keamanan dan keamanan privasi pengguna juga menjadi prioritas utama dalam situs tersebut sehingga para pemain dapat bermain dengan tenang tanpa perlu khawatir akan data pribadi mereka.
Selain itu, Kantorbola juga memberikan berbagai bonus dan promo menarik bagi para pemain, seperti bonus deposit dan cashback yang dapat meningkatkan keuntungan bermain. Dengan pelayanan customer service yang responsif dan profesional, para pemain juga dapat mendapatkan bantuan yang dibutuhkan dengan cepat dan mudah. Dengan reputasi yang baik dan banyaknya testimonial positif dari para pemain, Kantorbola menjadi pilihan situs gaming online terbaik bagi para pecinta game di Indonesia.
Frequently Asked Question ( FAQ )
A : Apa yang dimaksud dengan Situs Gaming Online Terbaik Kantorbola?
Q : Situs Gaming Online Terbaik Kantorbola adalah platform online yang menyediakan berbagai jenis permainan game yang berkualitas dan menarik untuk dimainkan.
A : Apa saja jenis permainan yang tersedia di Situs Gaming Online Terbaik Kantorbola?
Q : Di Situs Gaming Online Terbaik Kantorbola, anda dapat menemukan berbagai jenis permainan seperti game slot, poker, roulette, blackjack, dan masih banyak lagi.
A : Bagaimana cara mendaftar di Situs Gaming Online Terbaik Kantorbola?
Q : Untuk mendaftar di Situs Gaming Online Terbaik Kantorbola, anda hanya perlu mengakses situs resmi mereka, mengklik tombol “Daftar” dan mengisi formulir pendaftaran yang disediakan.
A : Apakah Situs Gaming Online Terbaik Kantorbola aman digunakan untuk bermain game?
Q : Ya, Situs Gaming Online Terbaik Kantorbola telah memastikan keamanan dan kerahasiaan data para penggunanya dengan menggunakan sistem keamanan terkini.
A : Apakah ada bonus atau promo menarik yang ditawarkan oleh Situs Gaming Online Terbaik Kantorbola?
Q : Tentu saja, Situs Gaming Online Terbaik Kantorbola seringkali menawarkan berbagai bonus dan promo menarik seperti bonus deposit, cashback, dan bonus referral untuk para membernya. Jadi pastikan untuk selalu memeriksa promosi yang sedang berlangsung di situs mereka.
Почему наши сигналы – всегда идеальный вариант:
Наша группа постоянно в тренде последних курсов и событий, которые воздействуют на криптовалюты. Это способствует команде оперативно реагировать и подавать актуальные трейды.
Наш состав обладает глубоким знанием анализа и умеет выделить крепкие и незащищенные аспекты для вступления в сделку. Это способствует минимизации опасностей и увеличению прибыли.
Вместе с командой мы применяем собственные боты-анализаторы для просмотра графиков на все интервалах. Это содействует нам доставать понятную картину рынка.
Перед публикацией сигнал в нашем канале Telegram команда осуществляем педантичную ревизию все сторон и подтверждаем допустимая длинный или краткий. Это обеспечивает надежность и качественность наших подач.
Присоединяйтесь к нам к нашему каналу прямо сейчас и достаньте доступ к подтвержденным торговым подачам, которые содействуют вам достигнуть финансовых результатов на рынке криптовалют!
https://t.me/Investsany_bot
Почему наши сигналы – всегда наилучший выбор:
Мы утром и вечером, днём и ночью на волне актуальных трендов и событий, которые воздействуют на криптовалюты. Это дает возможность нашей команде оперативно действовать и подавать актуальные подачи.
Наш коллектив обладает профундным понимание анализа и способен выделить крепкие и уязвимые факторы для присоединения в сделку. Это способствует для снижения угроз и увеличению прибыли.
Мы применяем личные боты для анализа для просмотра графиков на всех интервалах. Это помогает нашим специалистам получить полноценную картину рынка.
Перед приведением сигнал в нашем Telegram мы осуществляем внимательную проверку все аспектов и подтверждаем возможный длинный или краткий. Это подтверждает верность и качество наших сигналов.
Присоединяйтесь к нашему каналу к нашей группе прямо сейчас и достаньте доступ к подтвержденным торговым подачам, которые помогут вам вам достигнуть успеха в финансах на крипторынке!
https://t.me/Investsany_bot
canadian pharmacy: International Pharmacy delivery – reddit canadian pharmacy
veganchoicecbd.com
왕노인은 깜짝 놀라며 매우 의아해하며 물었다.
http://diflucan.icu/# diflucan 150 mg caps
tamoxifen for gynecomastia reviews: nolvadex side effects – tamoxifen for breast cancer prevention
where can i get diflucan: diflucan pill canada – medicine diflucan price
buy doxycycline without prescription uk: doxycycline 100 mg – generic for doxycycline
Intro
betvisa bangladesh
Betvisa bangladesh | Super Cricket Carnival with Betvisa!
IPL Cricket Mania | Kick off Super Cricket Carnival with bet visa.com
IPL Season | Exclusive 1,50,00,000 only at Betvisa Bangladesh!
Crash Games Heroes | Climb to the top of the 1,00,00,000 bonus pool!
#betvisabangladesh
Preview IPL T20 | Follow Betvisa BD on Facebook, Instagram for awards!
betvisa affiliate Dream Maltese Tour | Sign up now to win the ultimate prize!
https://www.bvthethao.com/
#betvisabangladesh #betvisabd #betvisaaffiliate
#betvisaaffiliatesignup #betvisa.com
Vì sự cam kết về trải nghiệm cá cược tốt hơn nhất và dịch vụ khách hàng chuyên nghiệp, BetVisa hoàn toàn tự hào là điểm đến lý tưởng cho những ai nhiệt huyết trò chơi trực tuyến. Hãy đăng ký ngay hôm nay và bắt đầu hành trình của bạn tại BetVisa – nơi niềm vui và may mắn chính là điều tất yếu.
Khám phá Thế Giới Cá Cược Trực Tuyến với BetVisa!
BetVisa Vietnam, một trong những nền tảng hàng đầu tại châu Á, được thành lập vào năm 2017 và hoạt động dưới giấy phép của Curacao, đã đưa vào hơn 2 triệu người dùng trên toàn thế giới. Với lời hứa đem đến trải nghiệm cá cược an toàn và tin cậy nhất, BetVisa sớm trở thành lựa chọn hàng đầu của người chơi trực tuyến.
BetVisa không chỉ cung cấp các trò chơi phong phú như xổ số, sòng bạc trực tiếp, thể thao trực tiếp và thể thao điện tử, mà còn mang đến cho người chơi những ưu đãi hấp dẫn. Thành viên mới đăng ký sẽ được tặng ngay 5 vòng quay miễn phí và có cơ hội giành giải thưởng lớn.
Đặc biệt, BetVisa hỗ trợ nhiều cách thức thanh toán linh hoạt như Betvisa Vietnam, cùng với các ưu đãi độc quyền như thưởng chào mừng lên đến 200%. Bên cạnh đó, hàng tuần còn có các chương trình khuyến mãi độc đáo như chương trình giải thưởng Sinh Nhật và Chủ Nhật Mua Sắm Điên Cuồng, mang đến cho người chơi cơ hội thắng lớn.
diflucan 150 mg tablet price in india: diflucan 150 mg price uk – diflucan usa
nolvadex vs clomid: tamoxifen bone density – tamoxifen breast cancer
purchase cipro: ciprofloxacin – buy cipro online canada
https://misoprostol.top/# buy cytotec
buy misoprostol over the counter Abortion pills online buy cytotec in usa
外送茶
現代社會,快遞已成為大眾化的服務業,吸引了許多人的注意和參與。 與傳統夜店、酒吧不同,外帶提供了更私密、便捷的服務方式,讓人們有機會在家中或特定地點與美女共度美好時光。
多樣化選擇
從台灣到日本,馬來西亞到越南,外送業提供了多樣化的女孩選擇,以滿足不同人群的需求和喜好。 無論你喜歡什麼類型的女孩,你都可以在外賣行業找到合適的女孩。
不同的價格水平
價格範圍從實惠到豪華。 無論您的預算如何,您都可以找到適合您需求的女孩,享受優質的服務並度過愉快的時光。
快遞業高度重視安全和隱私保護,提供多種安全措施和保障,讓客戶放心使用服務,無需擔心個人資訊外洩或安全問題。
如果你想成為一名經驗豐富的外包司機,外包產業也將為你提供廣泛的選擇和專屬服務。 只需按照步驟操作,您就可以輕鬆享受快遞行業帶來的樂趣和便利。
蓬勃發展的快遞產業為人們提供了一種新的娛樂休閒方式,讓人們在忙碌的生活中得到放鬆,享受美好時光。
robot 88
doxycycline 100mg tablets: odering doxycycline – doxycycline pills
doxycycline prices generic doxycycline where to purchase doxycycline
cytotec online: cytotec pills buy online – cytotec pills buy online
https://doxycyclinest.pro/# doxycycline hyc
I truly wanted to construct a simple remark to appreciate you for those fabulous tricks you are giving out at this website. My prolonged internet research has at the end been compensated with brilliant facts and strategies to write about with my pals. I ‘d assert that many of us readers are extremely endowed to dwell in a superb network with very many perfect people with very beneficial tactics. I feel pretty grateful to have come across your entire webpages and look forward to plenty of more amazing times reading here. Thank you once again for all the details.
otraresacamas.com
このように実用的な記事は他にはない。本当に役に立ちます。
Intro
betvisa philippines
Betvisa philippines | The Filipino Carnival, Spinning for Treasures!
Betvisa Philippines Surprises | Spin daily and win ₱8,888 Grand Prize!
Register for a chance to win ₱8,888 Bonus Tickets! Explore Betvisa.com!
Wild All Over Grab 58% YB Bonus at Betvisa Casino! Take the challenge!
#betvisaphilippines
Get 88 on your first 50 Experience Betvisa Online’s Bonus Gift!
Weekend Instant Daily Recharge at betvisa.com
https://www.88betvisa.com/
#betvisaphilippines #betvisaonline #betvisacasino
#betvisacom #betvisa.com
Nền tảng cá cược – Điểm Đến Tuyệt Vời Cho Người Chơi Trực Tuyến
Khám Phá Thế Giới Cá Cược Trực Tuyến với BetVisa!
Dịch vụ được thiết lập vào năm 2017 và vận hành theo chứng chỉ trò chơi Curacao với hơn 2 triệu người dùng. Với lời hứa đem đến trải nghiệm cá cược an toàn và tin cậy nhất, BetVisa nhanh chóng trở thành lựa chọn hàng đầu của người chơi trực tuyến.
Dịch vụ không chỉ đưa ra các trò chơi phong phú như xổ số, sòng bạc trực tiếp, thể thao trực tiếp và thể thao điện tử, mà còn mang lại cho người chơi những phần thưởng hấp dẫn. Thành viên mới đăng ký sẽ được tặng ngay 5 vòng quay miễn phí và có cơ hội giành giải thưởng lớn.
Nền tảng cá cược hỗ trợ nhiều phương thức thanh toán linh hoạt như Betvisa Vietnam, cùng với các ưu đãi độc quyền như thưởng chào mừng lên đến 200%. Bên cạnh đó, hàng tuần còn có các chương trình khuyến mãi độc đáo như chương trình giải thưởng Sinh Nhật và Chủ Nhật Mua Sắm Điên Cuồng, mang lại cho người chơi cơ hội thắng lớn.
Với sự cam kết về trải nghiệm cá cược tốt nhất và dịch vụ khách hàng chuyên nghiệp, BetVisa tự tin là điểm đến lý tưởng cho những ai đam mê trò chơi trực tuyến. Hãy đăng ký ngay hôm nay và bắt đầu hành trình của bạn tại BetVisa – nơi niềm vui và may mắn chính là điều tất yếu!
qiyezp.com
누구나 그의 안배에 정직하게 순종할 수 있을 뿐입니다.
prednisone over the counter australia prednisone 3 tablets daily 60 mg prednisone daily
http://prednisonea.store/# ordering prednisone
stromectol ivermectin tablets: ivermectin 3mg dosage – buy ivermectin cream for humans
http://stromectola.top/# ivermectin 1
how to get prednisone tablets: prednisone oral – cost of prednisone 5mg tablets
buy amoxicillin online mexico: buy cheap amoxicillin – amoxicillin without prescription
mexican prescription drugs online: no prescription drugs – prescription canada
https://onlinepharmacyworld.shop/# online pharmacy without prescription
canadian prescriptions in usa: buy drugs without prescription – canadian prescription drugstore reviews
erectile dysfunction pills online ed medications cost low cost ed medication
https://edpill.top/# erectile dysfunction pills online
https://medicationnoprescription.pro/# buy medication online with prescription
buying prescription drugs online from canada: buy prescription drugs on line – non prescription pharmacy
bmipas.com
この記事が大好きです。とても参考になります。
https://medicationnoprescription.pro/# overseas online pharmacy-no prescription
casino tr?c tuy?n casino tr?c tuy?n uy tin casino tr?c tuy?n uy tin
https://casinvietnam.com/# casino online uy tin
https://casinvietnam.com/# casino tr?c tuy?n
werankcities.com
Hongzhi 황제는 “나는 이미 도시에 들어갔고 곧 Dudu ‘s Mansion에 도착할 것입니다. “라고 말했습니다.